题目内容
11．函数$f（x）=-\frac{2}{x+1}$在（2，+∞）上的最小值是（ ）| A． | -2 | B． | $-\frac{2}{3}$ | C． | $-\frac{3}{2}$ | D． | 无最小值 |
分析 根据分式函数的单调性进行求解即可．
解答 解：∵函数$f（x）=-\frac{2}{x+1}$在（2，+∞）上为增函数，
∴$f（x）=-\frac{2}{x+1}$在（2，+∞）上没有最小值，
故选：D
点评 本题主要考查函数最值的求解，根据分式函数的单调性是解决本题的关键．比较基础．
练习册系列答案
世纪百通期末金卷系列答案
相关题目
1．已知a，b，c依次成等比数列，则不等式ax2+bx+c＞0的解集是（ ）
| A． | ∅ | B． | R | C． | {x|x≠-$\frac{b}{2a}$} | D． | 与a的正负有关 |
2．集合A={x|y=lg（1-x）}，B={a|关于x的方程x2-2x+a=0有实解}，则A∩B=（ ）
| A． | ∅ | B． | （-∞，1） | C． | [0，1） | D． | （0，1] |
19．函数f（x）=ax3+bx2+cx+d的部分数值如表：
则函数y=lgf（x）的定义域为（-1，1）∪（2，+∞）．
| x | -3 | -2 | -1 | 0 | 1 | 2 | 3 | 4 | 5 |
| f（x） | -80 | -24 | 0 | 4 | 0 | 0 | 16 | 60 | 144 |
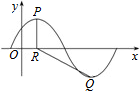已知函数f（x）=Asin（$\frac{π}{3}$x+φ），（A＞0，0＜φ＜$\frac{π}{2}$），y=f（x）的部分图象如图所示，P，Q分别为该图象上相邻的最高点和最低点，点P在x轴上的射影为R（1，0），cos∠PRQ=-$\frac{4}{5}$
3．5名高中毕业生报考三所重点院校，每人限报且只报一所院校，则不同的报名方法有（ ）
| A． | 35种 | B． | 53种 | C． | 60种 | D． | 10种 |
已知函数$f（x）=Asin（ωx+φ）（x∈R，ω＞0，0＜φ＜\frac{π}{2}）$的部分图象如图所示．