题目内容
【题目】已知函数![]() ,其中
,其中![]() .
.
(Ⅰ) 当a=-1时,求证: ![]() ;
;
(Ⅱ) 对任意![]() ,存在
,存在![]() ,使
,使![]() 成立,求a的取值范围.(其中e是自然对数的底数,e=2.71828…)
成立,求a的取值范围.(其中e是自然对数的底数,e=2.71828…)
【答案】(Ⅰ)详见解析(Ⅱ)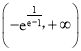
【解析】试题分析:
(1)利用题意证得函数的最大值为![]() 即可证得结论;
即可证得结论;
(2)首先利用分析法真理要证明的不等式,然后构造函数证明结论即可.
试题解析:
(Ⅰ)当 a=-1时, ![]() (x>-1),
(x>-1),
则![]() ,令
,令![]() ,得
,得![]() .
.
当![]() 时,
时, ![]() ,
, ![]() 单调递增;当
单调递增;当![]() 时,
时, ![]() ,
, ![]() 单调递减.
单调递减.
故当![]() 时,函数
时,函数![]() 取得极大值,也为最大值,所以
取得极大值,也为最大值,所以![]() ,
,
所以, ![]() ,得证.
,得证.
(Ⅱ)不等式![]() ,
,
即为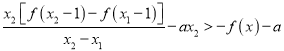 .
.
而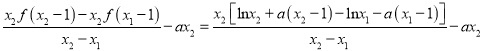
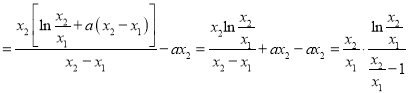 .
.
令![]() .故对任意
.故对任意![]() ,存在
,存在![]() ,使
,使![]() 恒成立,
恒成立,
所以![]() .
.
设![]() ,则
,则![]() ,
,
设![]() ,知
,知![]() 对于
对于![]() 恒成立,
恒成立,
则![]() 为
为![]() 上的增函数,于是
上的增函数,于是![]() ,
,
即![]() 对于
对于![]() 恒成立,所以
恒成立,所以![]() 为
为![]() 上的增函数.
上的增函数.
所以![]()
设![]() ,即
,即![]() ,
,
当a≥0时, ![]() 为
为![]() 上的减函数,且其值域为R,可知符合题意.
上的减函数,且其值域为R,可知符合题意.
当a<0时, ![]() ,由
,由![]() 可得
可得![]() ,
,
由![]() 得
得![]() ,则p(x)在
,则p(x)在![]() 上为增函数;由
上为增函数;由![]() 得
得![]() ,则p(x)在
,则p(x)在![]() 上为减函数,所以
上为减函数,所以![]() .
.
从而由![]() ,解得
,解得![]() .
.
综上所述,a的取值范围是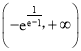 .
.

【题目】为了调查“五一”小长假出游选择“有水的地方”是否与性别有关,现从该市“五一”出游旅客中随机抽取500人进行调查,得到如下2×2列联表:(单位:人)
选择“有水的地方” | 不选择“有水的地方” | 合计 | |
男 | 90 | 110 | 200 |
女 | 210 | 90 | 300 |
合计 | 300 | 200 | 500 |
(Ⅰ)据此样本,有多大的把握认为选择“有水的地方”与性别有关;
(Ⅱ)若以样本中各事件的频率作为概率估计全市“五一”所有出游旅客情况,现从该市的全体出游旅客(人数众多)中随机抽取3人,设3人中选择“有水的地方”的人数为随机变量X,求随机变量X的数学期望和方差.
附临界值表及参考公式:
P(K2≥k0) | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
k0 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
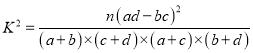 ,n=a+b+c+d.
,n=a+b+c+d.
【题目】某社区为丰富居民节日活动,组织了“迎新春”象棋大赛,已知报名的选手情况统计如下表:
组别 | 男 | 女 | 总计 |
中年组 |
|
| 91 |
老年组 | 16 |
|
|
已知中年组女性选手人数是仅比老年组女性选手人数多2人.若对中年组和老年组分别利用分层抽样的方法抽取部分报名者参加比赛,已知老年组抽取了5人,其中女性3人,中年组抽取了7人.
(Ⅰ)求表格中的数据![]() ;
;
(Ⅱ)若从选出的中年组的选手中随机抽取两名进行比赛,求至少有一名女性选手的概率.