题目内容
f (x)=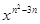 (n∈Z)是偶函数,且y=f(x)在(0,+∞)上是减函数,则n=( ).
(n∈Z)是偶函数,且y=f(x)在(0,+∞)上是减函数,则n=( ).
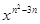 (n∈Z)是偶函数,且y=f(x)在(0,+∞)上是减函数,则n=( ).
(n∈Z)是偶函数,且y=f(x)在(0,+∞)上是减函数,则n=( ).| A.1 | B.2 | C.1或2 | D.3 |
C
试题分析:结合幂函数的性质可知,若f(x)=x
 (n∈Z)是偶函数且在(0,+∞)上是减函数,结合n2-3n为整数,可知,n2-3n<0,且n2-3n为偶数,可求.
(n∈Z)是偶函数且在(0,+∞)上是减函数,结合n2-3n为整数,可知,n2-3n<0,且n2-3n为偶数,可求.:∵f(x)=x
 (n∈Z)是偶函数,且n2-3n为整数,∴n2-3n为偶数,又∵y=f(x)在(0,+∞)上是减函数,由幂函数的性质可知,n2-3n<0,即0<n<3
(n∈Z)是偶函数,且n2-3n为整数,∴n2-3n为偶数,又∵y=f(x)在(0,+∞)上是减函数,由幂函数的性质可知,n2-3n<0,即0<n<3∵n∈Z,则n=1或n=2
当n=1时,n2-3n=-2符合题意;当n=2时,n2-3n=-2,符合题意
故n=1或n=2
故选C
点评:解答本题的关键是熟练掌握幂函数的性质并能灵活应用.注意幂函数的指数大于零,在第一象限内递增,小于零时,则递减。

练习册系列答案
 怎样学好牛津英语系列答案
怎样学好牛津英语系列答案 导学教程高中新课标系列答案
导学教程高中新课标系列答案
相关题目
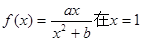 处取得极值2。
处取得极值2。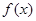 的解析式;
的解析式; 为增函数;
为增函数;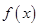 是偶函数,且
是偶函数,且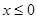 时,
时,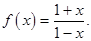 。
。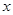 >0时
>0时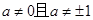 ,证明:
,证明: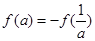
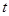 百件时,若
百件时,若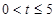 ,则销售所得的收入为
,则销售所得的收入为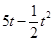 万元:若
万元:若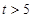 ,则销售收入为
,则销售收入为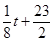 万元.
万元.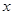 百件
百件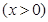 ,请把该公司生产并销售这种产品所得的年利润
,请把该公司生产并销售这种产品所得的年利润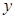 表示为当年生产量
表示为当年生产量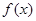 是定义在
是定义在 上的单调增函数,满足
上的单调增函数,满足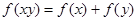 ,
,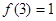 ,
,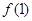 ;
;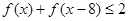 ,求
,求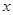 的取值范围。
的取值范围。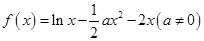 存在单调递减区间,则实数
存在单调递减区间,则实数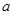 的取值
的取值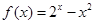 ,问方程
,问方程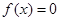 在区间[-1,0]内是否有
在区间[-1,0]内是否有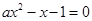 在(0,1)内恰有一解,求实数
在(0,1)内恰有一解,求实数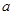 的取值范围.
的取值范围.  上是增函数,那么实数a的取值范围是( )
上是增函数,那么实数a的取值范围是( )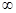 )
)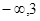 )
)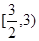
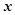 的函数
的函数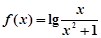 ,有下列结论:
,有下列结论: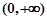 ; ②、该函数是奇函数;
; ②、该函数是奇函数;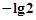 ;
;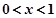 时
时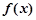 为增函数,当
为增函数,当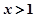 时
时