题目内容
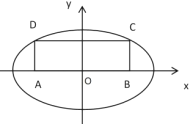
【题目】如图，在矩形
中，
，
，以
，
为焦点的椭圆
：
恰好过
，
两点.
（1）求椭圆的方程；
（2）已知
为原点，直线
：
与
轴交于点
，与椭圆相交于
、
两点，且、在轴异侧，若
，求
的取值范围.
【答案】（1）
（2）
或
.
【解析】
（1）根据矩形的边长，结合椭圆的性质即可求得
的值，进而求得椭圆的标准方程.
（2）联立直线与椭圆方程，化简方程并由韦达定理可得
，
，由直线与圆相交可得
，并由题意可设
，
及
，再由
求得
的范围；由
，分别求得面积后代入，结合韦达定理即可求得
，综合即可得的取值范围.
（1）∵
，
，
∴
，
，
，
解得
，
，
∴椭圆的方程为.
（2）联立直线与椭圆方程，
，
化简可得
，
∵直线与椭圆相交，∴
，
化简变形可得
①，
∵设，，不妨设，
②，
③.
由，得
，
∵
，
，且，
则
，去掉绝对值，则
④
联立②④，得
，
，
代入③得
，化简可得
，
代入①式有
，化简可得，
所以的范围为或.
练习册系列答案
相关题目
