Question

【题目】[选修4-4：坐标系与参数方程]

在直角坐标系中，曲线的参数方程为（为参数），以原点为极点，轴的正半轴为极轴建立极坐标系，曲线的极坐标方程为．

（1）写出曲线的普通方程和曲线的直角坐标方程；

（2）已知点是曲线上的动点，求点到曲线的最小距离．

Answer 1

【答案】（1）（2）

【解析】

(1) 曲线C1的参数方程消去参数，能求出曲线C1的普通方程，曲线C2的极坐标方程利用，能求出曲线C2的直角坐标方程；(2) 设点的坐标为，利用点到直线的距离表示点到曲线的最小距离，结合三角函数的图像与性质即可得到最小值.

（1）消去参数得到，

故曲线的普通方程为

，由

得到，

即,故曲线的普通方程为

（2）〖解法1〗设点的坐标为，

点到曲线的距离

所以，当时，的值最小，

所以点到曲线的最小距离为.

（2）〖解法2〗设平行直线：的直线方程为

当直线与椭圆相切于点P时，P到直线的距离取得最大或最小值。

由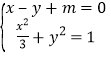得，

令其判别式，解得，

经检验，当时，点P到直线的距离最小，最小值为

所以点到曲线的最小距离为.