题目内容
如图,在长方体ABCD—A1B1C1D1中,AB=2,BB1=BC=1,E为D1C1的中点,连结ED,EC,EB和DB.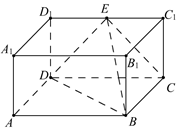
(1)求证:ED⊥平面EBC;
(2)求三棱锥E-DBC的体积.
(1)见解析;(2)
解析试题分析:
(1)易得△DD1E为等腰直角三角形 DE⊥EC,BC⊥平面
DE⊥EC,BC⊥平面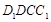
 BC⊥DE,所以DE⊥平面EBC
BC⊥DE,所以DE⊥平面EBC 平面DEB⊥平面EBC.
平面DEB⊥平面EBC.
(2)需要做辅助线,取CD中点M,连接EM
 ∥
∥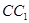 ,
, DCB
DCB 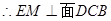 (这个证明很关键),然后根据公式
(这个证明很关键),然后根据公式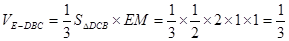 .
.
试题解析:
(1)在长方体ABCD-A1B1C1D1中,AB=2,BB1=BC=1,E为D1C1的中点.
∴△DD1E为等腰直角三角形,∠D1ED=45°.同理∠C1EC=45°.
∴ ,即DE⊥EC.
,即DE⊥EC.
在长方体ABCD- 中,BC⊥平面
中,BC⊥平面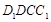 ,又DE
,又DE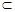 平面
平面 ,
,
∴BC⊥DE.又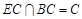 ,
,
∴DE⊥平面EBC.又
∴平面DEB⊥平面EBC.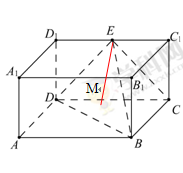
(2)取CD中点M,连接EM, E为D1C1的中点,
E为D1C1的中点, ∥
∥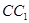 ,且
,且 ,
,  又
又 DCB
DCB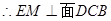
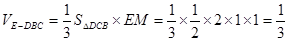 .
.
考点:线面垂直,三棱锥的体积.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 平面PCD;
平面PCD;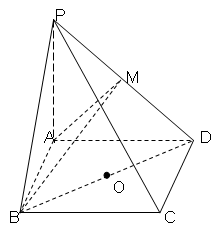
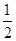 PD.
PD.
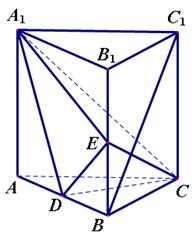
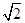 ,求三棱锥D一A1CE的体积.
,求三棱锥D一A1CE的体积. 中,已知
中,已知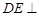 平面
平面 ,
,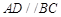 ,
,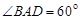 ,
,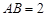 ,
,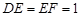 .
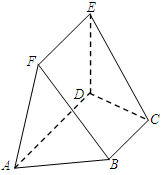
.
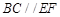 ;
;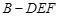 的体积.
的体积.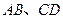 的长度分别等于
的长度分别等于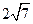 、
、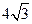 ,每条弦的两端都在球面上运动,则两弦中点之间距离的最大值为 .
,每条弦的两端都在球面上运动,则两弦中点之间距离的最大值为 .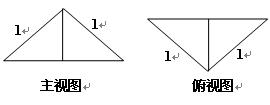
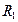 ,
,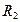 ,
,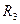 满足
满足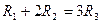 ,则它们的表面积
,则它们的表面积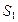 ,
,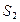 ,
,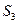 ,满足的等量关系是___________.
,满足的等量关系是___________.