题目内容
如图,在四棱锥P-ABCD中,底面ABCD是矩形,PA⊥平面ABCD,PA=AD=4,AB=2,以BD的中点O为球心、BD为直径的球面交PD于点M.
(1)求证:平面ABM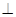 平面PCD;
平面PCD;
(2)求三棱锥M-ABD的体积.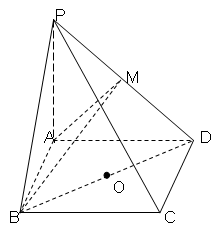
(1)见解析(2)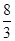
解析试题分析:(1)由PA⊥平面ABCD知,PA⊥AB,由ABCD为矩形知,AB⊥AD,由线面垂直判定定理知,AB⊥PAD,所以PB⊥AB,由以BD为直径的球与PB的交点为M知,BM⊥DM,由线面垂直判定知PD⊥面ABM,由面面垂直判定定理知面PCD⊥面ABM;(2)由(1)知,PD⊥面ABM,所以PD⊥AM,因为PA=AD=4,所以M是PD的中点,取AD的中点为N,则NM平行PA,因为PA⊥平面ABCD,所以MN⊥ABCD,MN= =2,即MN是三棱锥M-ABD的高,用棱锥的体积公式即可求出其体积.
=2,即MN是三棱锥M-ABD的高,用棱锥的体积公式即可求出其体积.
试题解析:(1)

又


由题意得 ,
,

又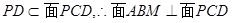 6分
6分
(2)由(1)知,PD⊥面ABM,所以PD⊥AM,
因为PA=AD=4,所以M是PD的中点,
取AD的中点为N,则NM平行PA,
因为PA⊥平面ABCD,所以MN⊥ABCD,MN= =2,
=2,
所以 =
=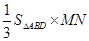 =
= =
=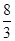 . 12分
. 12分
考点:球的性质,线面垂直的判定与性质,面面垂直判定定理,棱锥的体积公式,逻辑推论证能力.

练习册系列答案
相关题目
 和它的三视图.
和它的三视图.
 是线段
是线段 上的一点,且
上的一点,且 ,求证:
,求证: ;
; 的余弦值.
的余弦值.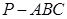 ,其表面展开图是三角形
,其表面展开图是三角形 ,如图,求△
,如图,求△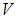 .
.


 ,M是线段AE上的动点.
,M是线段AE上的动点.
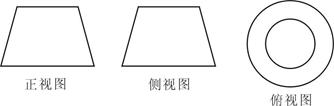
 出该几何体的名称是 .
出该几何体的名称是 .