题目内容
7．
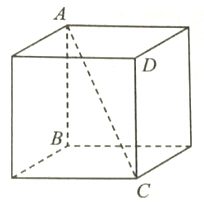如图所示，在棱长为1的正方体内有两个球相外切且又分别与正方体内切，求两球半径之和．
分析 利用ABCD为过球心的对角面，即可求两球半径之和．
解答 解：如图，ABCD为过球心的对角面，AC=$\sqrt{3}$，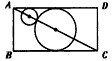
设两球半径为R、r，则有R+r+$\sqrt{3}$（R+r）=$\sqrt{3}$，
所以R+r=$\frac{3-\sqrt{3}}{2}$．
点评 本题是基础题，考查正方体的内接体的知识，解题关键在ABCD为过球心的对角面，是常考题型．
练习册系列答案
尖子生新课堂课时作业系列答案
英才计划同步课时高效训练系列答案
相关题目
17．编号分别为A1，A2，A3，…，A12的12名篮球运动员在某次篮球比赛中的得分记录如下：
（1）完成如下的频率分布表：
（2）从得分在区间[10，20）内的运动员中随机抽取2人，求这2人得分之和大于30的概率．
| 运动员编号 | A1 | A2 | A3 | A4 | A5 | A6 | A7 | A8 | A9 | A10 | A11 | A12 |
| 得分 | 5 | 10 | 12 | 16 | 8 | 21 | 27 | 15 | 6 | 22 | 18 |
| 得分区间 | 频数 | 频率 |
| [0，10） | 3 | $\frac{1}{4}$ |
| [10，20） | ||
| [20，30） | ||
| 合计 | 12 | 1.00 |