题目内容
【题目】为建立健全国家学生体质健康监测评价机制,激励学生积极参加身体锻炼,教育部印发《国家学生体质健康标准(2014年修订)》,要求各学校每学年开展覆盖本校各年级学生的《标准》测试工作.为做好全省的迎检工作,某市在高三年级开展了一次体质健康模拟测试(健康指数满分100分),并从中随机抽取了200名学生的数据,根据他们的健康指数绘制了如图所示的频率分布直方图.

(1)估计这200名学生健康指数的平均数![]() 和样本方差
和样本方差![]() (同一组数据用该组区间的中点值作代表);
(同一组数据用该组区间的中点值作代表);
(2)由频率分布直方图知,该市学生的健康指数![]() 近似服从正态分布
近似服从正态分布![]() ,其中
,其中![]() 近似为样本平均数
近似为样本平均数![]() ,
,![]() 近似为样本方差
近似为样本方差![]() .
.
①求![]() ;
;
②已知该市高三学生约有10000名,记体质健康指数在区间![]() 的人数为
的人数为![]() ,试求
,试求![]() .
.
附:参考数据![]() ,
,
若随机变量![]() 服从正态分布
服从正态分布![]() ,则
,则![]() ,
,![]() ,
,![]() .
.
【答案】(1)75,135;(2)①![]() ;②
;②![]() .
.
【解析】
(1)以组中值代替小组平均值,根据加权平均数公式计算平均数![]() ,根据方差公式计算
,根据方差公式计算![]() ;
;
(2)①利用正态分布的性质求得![]() ;
;
②根据二项分布的期望公式得出![]() .
.
(1)由频率分布直方图可知,各区间对应的频数分布表如下:
分值区间 |
|
|
|
|
|
|
频数 | 5 | 15 | 40 | 75 | 45 | 20 |
∴![]() ,
,
![]()
![]() .
.
(2)①由(1)知![]() 服从正态分布
服从正态分布![]() ,且
,且![]() ,
,
∴![]() .
.
②依题意,![]() 服从二项分布,即
服从二项分布,即![]() ~
~![]() ,则
,则![]() .
.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
【题目】某公司为了提高利润,从2014年至2018年每年对生产环节的改进进行投资,投资金额与年利润增长的数据如下表:
年份 | 2014 | 2015 | 2016 | 2017 | 2018 |
投资金额x(万元) | 5 | 5.5 | 6 | 6.5 | 7 |
年利润增长y(万元) | 7.5 | 8 | 9 | 10 | 11.5 |
(1)请用最小二乘法求出y关于x的回归直线方程;
(2)如果2020年该公司计划对生产环节的改进的投资金额为8万元,估计该公司在该年的年利润增长为多少?
参考公式: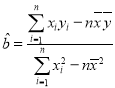 ,
,![]() 参考数据:
参考数据:![]() ,
,![]()