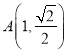题目内容
【题目】已知点![]() ,椭圆
,椭圆![]() 的离心率为
的离心率为![]() ,
,![]() 是椭圆
是椭圆![]() 的右焦点,直线
的右焦点,直线![]() 的斜率为
的斜率为![]() ,
,![]() 为坐标原点.
为坐标原点.
(1)求![]() 的方程;
的方程;
(2)设过点![]() 的动直线
的动直线![]() 与
与![]() 相交于
相交于![]() 两点,问:是否存在直线
两点,问:是否存在直线![]() ,使以
,使以![]() 为直径的圆经过原点
为直径的圆经过原点![]() ,若存在,求出对应直线
,若存在,求出对应直线![]() 的方程,若不存在,请说明理由.
的方程,若不存在,请说明理由.
【答案】(1)![]() ;(2)
;(2)![]() 或
或![]() .
.
【解析】试题分析:(1)设出![]() ,由直线
,由直线![]() 的斜率为
的斜率为![]() 求得
求得![]() ,结合离心率求得
,结合离心率求得![]() ,再由隐含条件求得
,再由隐含条件求得![]() ,则椭圆方程可求;(2)当
,则椭圆方程可求;(2)当![]() 轴时,不合题意;当直线
轴时,不合题意;当直线![]() 斜率存在时,设直线
斜率存在时,设直线![]() :
:![]() 代入椭圆方程化简,由判别式大于
代入椭圆方程化简,由判别式大于![]() 求得
求得![]() 的范围,若存在以
的范围,若存在以![]() 为直径的圆经过点原点
为直径的圆经过点原点![]() ,求出
,求出![]() ,即
,即![]() ,得到
,得到![]() ,符合
,符合![]() ,进一步求出
,进一步求出![]() 值,则直线方程可求得.
值,则直线方程可求得.
试题解析:(1)设![]() ,由条件知,
,由条件知, ![]() ,得
,得![]() .
.
又![]() ,所以
,所以![]() ,
,
![]() .
.
故![]() 的方程为
的方程为![]() .
.
(2)当![]() 垂直于
垂直于![]() 轴时不合题意,故设
轴时不合题意,故设![]() ,
,![]() .
.
将![]() 代入
代入![]() ,得
,得![]() .
.
当![]() ,即
,即![]() 时,
时,
![]() ,
,![]() ,
,
所以![]() .
.
若存在以![]() 为直径的圆经过点原点
为直径的圆经过点原点![]() ,则
,则![]() ,
,
即![]() ,即
,即![]() ,
,
所以![]() ,符合
,符合![]() ,所以存在
,所以存在![]() ,符合题意,
,符合题意,
此时![]() 或
或![]() .
.

练习册系列答案
 开心练习课课练与单元检测系列答案
开心练习课课练与单元检测系列答案 开心试卷期末冲刺100分系列答案
开心试卷期末冲刺100分系列答案 双基同步导航训练系列答案
双基同步导航训练系列答案
相关题目
【题目】某校100名学生期中考试数学成绩的频率分布直方图如图,其中成绩分组区间如下:
组号 | 第一组 | 第二组 | 第三组 | 第四组 | 第五组 |
分组 | [50,60) | [60,70) | [70,80) | [80,90) | [90,100] |
(1)求图中a的值;
(2)根据频率分布直方图,估计这100名学生期中考试数学成绩的平均分;
(3)现用分层抽样的方法从第3、4、5组中随机抽取6名学生,将该样本看成一个总体,从中随机抽取2名,求其中恰有1人的分数不低于90分的概率?