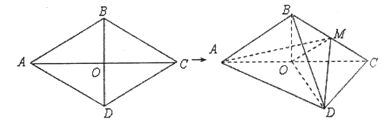
题目内容
【题目】已知椭圆![]() :
: ![]() 的左、右焦点分别为
的左、右焦点分别为![]() ,
, ![]() ,点
,点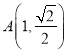 在椭圆
在椭圆![]() 上.
上.
(Ⅰ)求椭圆![]() 的标准方程;
的标准方程;
(Ⅱ)是否存在斜率为2的直线![]() ,使得当直线
,使得当直线![]() 与椭圆
与椭圆![]() 有两个不同交点
有两个不同交点![]() 、
、![]() 时,能在直线
时,能在直线![]() 上找到一点
上找到一点![]() ,在椭圆
,在椭圆![]() 上找到一点
上找到一点![]() ,满足
,满足![]() ?若存在,求出直线
?若存在,求出直线![]() 的方程;若不存在,说明理由.
的方程;若不存在,说明理由.
【答案】(1)![]() ;(2)不存在这样的点
;(2)不存在这样的点![]() ,理由见解析.
,理由见解析.
【解析】试题分析:(1)借助题设条件运用椭圆定义建立方程求解;(2)借助题设运用直线与椭圆的位置关系探求.
试题解析:
(1)设椭圆![]() 的焦距为
的焦距为![]() ,则
,则![]() ,
,
因为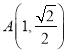 在椭圆
在椭圆![]() 上,所以
上,所以![]() ,
,
因此![]() ,
, ![]() ,故椭圆
,故椭圆![]() 的方程为
的方程为![]() .
.
(2)椭圆![]() 上不存在这样的点
上不存在这样的点![]() .证明如下:
.证明如下:
设直线![]() 的方程为
的方程为![]() ,
,
设![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() 的中点为
的中点为![]() ,
,
由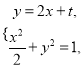 得
得![]() ,
,
所以![]() ,且
,且![]() ,故
,故![]() ,且
,且![]() ,
,
由![]() 知四边形
知四边形![]() 为平行四边形,
为平行四边形,
而![]() 为线段
为线段![]() 的中点,因此,
的中点,因此, ![]() 也是线段
也是线段![]() 的中点,
的中点,
所以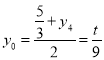 ,可得
,可得![]() ,
,
又![]() ,所以
,所以![]() ,
,
因此点![]() 不在椭圆上.
不在椭圆上.

【题目】刘老师是一位经验丰富的高三理科班班主任,经长期研究,他发现高中理科班的学生的数学成绩(总分150分)与理综成绩(物理、化学与生物的综合,总分300分)具有较强的线性相关性,以下是刘老师随机选取的八名学生在高考中的数学得分x与理综得分y(如下表):
学生编号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
数学分数x | 52 | 64 | 87 | 96 | 105 | 123 | 132 | 141 |
理综分数y | 112 | 132 | 177 | 190 | 218 | 239 | 257 | 275 |
参考数据及公式: ![]() .
.
(1)求出y关于x的线性回归方程;
(2)若小汪高考数学110分,请你预测他理综得分约为多少分?(精确到整数位);
(3)小金同学的文科一般,语文与英语一起能稳定在215分左右.如果他的目标是在
高考总分冲击600分,请你帮他估算他的数学与理综大约分别至少需要拿到多少分?(精确到整数位).
【题目】衡州市临枣中学高二某小组随机调查芙蓉社区160个人,以研究这一社区居民在20:00-22:00时间段的休闲方式与性别的关系,得到下面的数据表:
休闲方式 性别 | 看电视 | 看书 | 合计 |
男 | 20 | 100 | 120 |
女 | 20 | 20 | 40 |
合计 | 40 | 120 | 160 |
下面临界值表:
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
![]()
(Ⅰ)将此样本的频率估计为总体的概率,随机调查3名在该社区的男性,设调查的3人在这一时间段以看书为休闲方式的人数为随机变量![]() ,求
,求![]() 的分别列和期望;
的分别列和期望;
(Ⅱ)根据以上数据,能否有99%的把握认为“在20:00-22:00时间段的休闲方式与性别有关系”?
【题目】为了解某单位员工的月工资水平,从该单位500位员工中随机抽取了50位进行调查,得到如下频数分布表和频率分布直方图:
月工资 (单位:百元) | [15,25) | [25,35) | [35,45) | [45,55) | [55,65) | [65,75) |
男员工数 | 1 | 8 | 10 | 6 | 4 | 4 |
女员工数 | 4 | 2 | 5 | 4 | 1 | 1 |
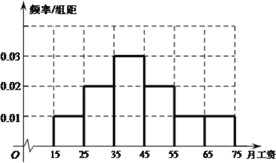
(1)![]() 试由上图估计该单位员工月平均工资;
试由上图估计该单位员工月平均工资;
(2)现用分层抽样的方法从月工资在![]() 和
和![]() 的两组所调查的男员工中随机选取5人,问各应抽取多少人?
的两组所调查的男员工中随机选取5人,问各应抽取多少人?
(3)若从月工资在![]() 和
和![]() 两组所调查的女员工中随机选取2人,试求这2人月工资差不超过1000元的概率.
两组所调查的女员工中随机选取2人,试求这2人月工资差不超过1000元的概率.
【题目】某中学举行了一次“环保知识竞赛”, 全校学生参加了这次竞赛.为了了解本次竞赛成绩情况,从中抽取了部分学生的成绩(得分取正整数,满分为100分)作为样本进行统计.请根据下面尚未完成并有局部污损的频率分布表和频率分布直方图(如图所示)解决下列问题:
![]()
| 分组 | 频数 | 频率 |
第1组 | [50,60) | 8 | 0 16 |
第2组 | [60,70) | a | ▓ |
第3组 | [70,80) | 20 | 0 40 |
第4组 | [80,90) | ▓ | 0 08 |
第5组 | [90,100] | 2 | b |
合计 | ▓ | ▓ |

(1)求出![]() 的值;
的值;
(2)在选取的样本中,从竞赛成绩是80分以上(含80分)的同学中随机抽取2名同学到广场参加环保知识的志愿宣传活动
(ⅰ)求所抽取的2名同学中至少有1名同学来自第5组的概率;
(ⅱ)求所抽取的2名同学来自同一组的概率