题目内容
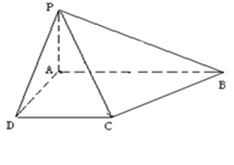
正方形ABCD中,点O是对角线AC的中点,点P是对角线AC上一动点.
(1)如图1,当点P在线段OA上运动时(不与点A、O重合) ,PE⊥PB交线段CD于点E,PF⊥CD于点E.
①判断线段DF、EF的数量关系,并说明理由;
②写出线段PC、PA、CE之间的一个等量关系,并证明你的结论;
(2)如图2,当点P在线段OC上运动时(不与点O、C重合),PE⊥PB交直线CD于点E,PF⊥CD于点E.判断(1)中的结论①、②是否成立?若成立,说明理由;若不成立,写出相应的结论并证明.
(1)①DF=EF ②PC-PA= CE
CE
(2)结论①成立, 结论②不成立,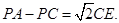
解析试题分析:(1)①DF=EF …1分
理由如下:连接PD,因为AB=AD,AP=AP,∠BAP=∠DAP=45°,
所以 ,
,
所以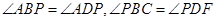 ,
,
因为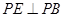 ,所以在四边形
,所以在四边形 中
中 ,
,
因为 ,所以
,所以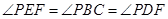 ,
,
因为 所以
所以 (等腰三角形底边垂线即底边平分线). …4分
(等腰三角形底边垂线即底边平分线). …4分
②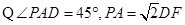 ,同理
,同理 ,
,
所以 ,
,
因为 所以
所以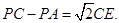 …7分
…7分
(2)结论①成立 …8分
理由同(1)①即可; …9分
结论②不成立. …10分
相应的结论为PA-PC= CE …11分
CE …11分
证明同(1)②. … 12分
考点:本小题主要考查平面图形中的探究性问题,考查学生综合运用平面几何知识解决问题的能力.
点评:对于此类问题,要灵活运用平面几何知识(平行、相似、全等等),要注意恰当转化.

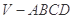 中,底面
中,底面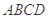 是正方形,侧面
是正方形,侧面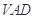 是正三角形,平面
是正三角形,平面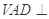 底面
底面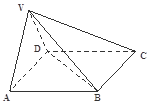
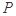 为线段VC的中点,求证:
为线段VC的中点,求证: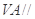 平面
平面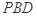 ;
;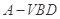 的体积
的体积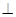 BQ并说明理由.
BQ并说明理由.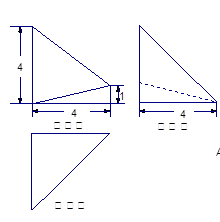
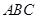 中,
中,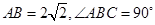 ,点
,点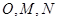 分别为线段
分别为线段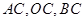 的中点,将
的中点,将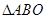 和
和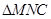 分别沿
分别沿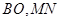 折起,使二面角
折起,使二面角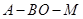 和二面角
和二面角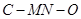 都成直二面角,如图(2)所示。
都成直二面角,如图(2)所示。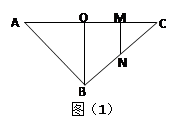

 面
面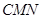 ;
;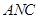 与平面
与平面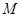 到平面
到平面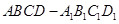 的底面边长为2,
的底面边长为2, .
.
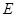 为线段
为线段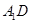 的中点,求
的中点,求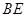 与平面
与平面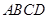 所成角的大小.
所成角的大小. 的正方体
的正方体 中分离出来的:
中分离出来的: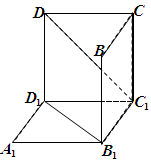
 是否在平面
是否在平面 内;(回答是与否)
内;(回答是与否)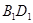 与
与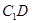 所成的角;
所成的角; 中,
中, 为底面圆的两条直径 ,AB交CD于O,且
为底面圆的两条直径 ,AB交CD于O,且 ,
, ,
, 为
为 的中点.
的中点.
 平面
平面 ;
; 与
与 所成角的正切值 .
所成角的正切值 .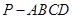 中,
中,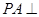 平面
平面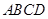 ,四边形
,四边形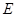 ,
,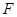 分别是
分别是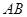 ,
,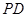 的中点.若
的中点.若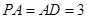 ,
,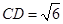 。
。
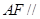 平面
平面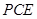 ;
;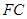 平面
平面 的底面为直角梯形,
的底面为直角梯形,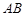 //
//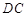 ,
,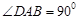 ,
,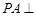 底面
底面 ,且
,且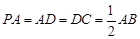 .
.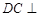 平面
平面 ;
; 的余弦值的大小.
的余弦值的大小.