题目内容
(本小题满分12分)
设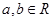 ,且
,且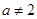 ,定义在区间
,定义在区间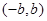 内的函数
内的函数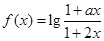 是奇函数.
是奇函数.
(1)求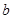 的取值范围;
的取值范围;
(2)讨论函数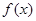 的单调性并证明.
的单调性并证明.
设
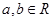 ,且
,且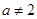 ,定义在区间
,定义在区间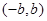 内的函数
内的函数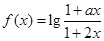 是奇函数.
是奇函数.(1)求
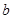 的取值范围;
的取值范围;(2)讨论函数
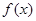 的单调性并证明.
的单调性并证明.(1)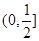 . (2)
. (2)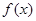 在(-b,b)内是减函数,具有单调性.
在(-b,b)内是减函数,具有单调性.
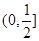 . (2)
. (2)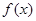 在(-b,b)内是减函数,具有单调性.
在(-b,b)内是减函数,具有单调性. 试题分析:(1)由函数f(x)在区间(-b,b)是奇函数,知f(-x)=-f(x),x∈(-b,b)上恒成立,用待定系数法求得a;同时函数要有意义,即
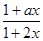 >0,x∈(-b,b)上恒成立,可解得结果.
>0,x∈(-b,b)上恒成立,可解得结果.(2)选用定义法求解,先任意取两个变量且界定大小,再作差变形看符号.
解 (1)
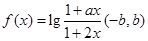 是奇函数等价于:
是奇函数等价于:对任意
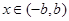 都有
都有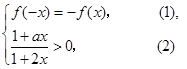 …………………2分
…………………2分(1)式即为
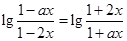 ,由此可得
,由此可得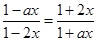 ,也即
,也即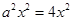 ,…………………4分
,…………………4分此式对任意
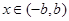 都成立相当于
都成立相当于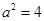 ,因为
,因为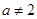 ,所以
,所以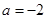 ,
,代入②式,得
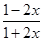 >0,即
>0,即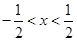 ,此式对任意
,此式对任意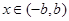 都成立相当于
都成立相当于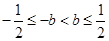 ,…………………6分
,…………………6分所以
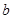 的取值范围是
的取值范围是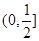 .…………………7分
.…………………7分(2)设任意的
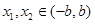 ,且
,且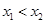 ,由
,由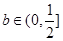 ,得
,得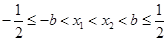 ,
,所以
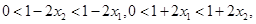 …………………9分
…………………9分从而
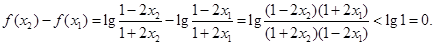

因此
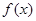 在(-b,b)内是减函数,具有单调性. …………………12分
在(-b,b)内是减函数,具有单调性. …………………12分点评:解决该试题的关键是要注意定义域优先考虑原则,以及作差时的变形要到位,要用上两个变量的大小关系。

练习册系列答案
 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案
相关题目
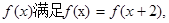 当
当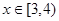 时,
时,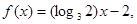 则
则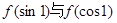 的大小关系为( )
的大小关系为( )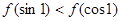
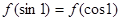
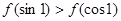
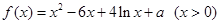
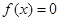 有三个不同的实根.
有三个不同的实根.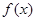 定义在实数集R上,
定义在实数集R上,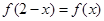 ,且当
,且当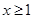 时
时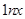 ,则有 ( )
,则有 ( )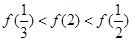
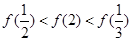
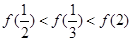
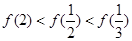
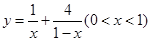 ,则
,则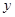 的最小值为 。
的最小值为 。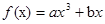 ,(
,(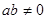 ),对任意
),对任意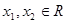 且
且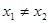 都有
都有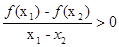 ,若
,若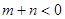 ,则
,则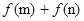 的值( )
的值( )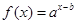 的图象如图所示,其中
的图象如图所示,其中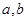 为常数,则下列结论正确的是
为常数,则下列结论正确的是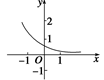
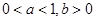
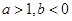
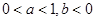
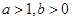
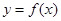 在区间
在区间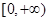 单调增加,则满足
单调增加,则满足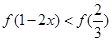 的
的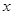 取值范围是( )
取值范围是( )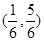
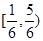
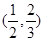
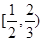
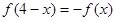 ,当x>2时,f(x)单调递增,如果x1+x2<4,且(x1-2)(x2-2)<0,则f(x1)+f(x2)的值( )
,当x>2时,f(x)单调递增,如果x1+x2<4,且(x1-2)(x2-2)<0,则f(x1)+f(x2)的值( )