题目内容
7．已知函数f（x）=${x}^{{n}^{2}-3n}$（n∈Z）是偶函数，且y=f（x）在（0，+∞）上是减函数，则n=1或2．分析 从单调性入手，则指数小于零，确定出n的范围，然后再通过偶函数验证得到n值．
解答 解：∵y=f（x）在（0，+∞）上是减函数，
∴n2-3n＜0，
∴0＜n＜3．
又∵是偶函数，
∴n=1或2．
故答案为：1或2．
点评 本题主要考查幂函数的单调性和奇偶性，单调性要充分利用好在第一象限内指数大于零为增函数，小于零为减函数，对称区间上的单调性用奇偶性来判断．
练习册系列答案
阅读快车系列答案
相关题目
3．
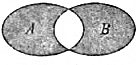如图所示的韦恩图中，A，B中两非空集合，定义集合A?B为阴影部分表示的集合，若x，y∈R，A={x|y=ln（2x-x2）}，B={y|y=ex，x＞0}，则A?B为（ ）
如图所示的韦恩图中，A，B中两非空集合，定义集合A?B为阴影部分表示的集合，若x，y∈R，A={x|y=ln（2x-x2）}，B={y|y=ex，x＞0}，则A?B为（ ）| A． | {x|0＜x＜2} | B． | {x|x≤1或x≥2} | C． | {x|0≤x≤1或x≥2} | D． | {x|0＜x≤1或x≥2} |
18．已知集合A={x|0＜x＜1|，B={x|-1≤log2x≤1}，则A∩B=（ ）
| A． | （0，2] | B． | [$\frac{1}{2}$，1） | C． | （1，2] | D． | [$\frac{1}{2}$，2] |