Question

【题目】( 本小题满分14)

如图，在三棱锥P—ABC中，PC⊥底面ABC，AB⊥BC，D，E分别是AB，PB的中点．

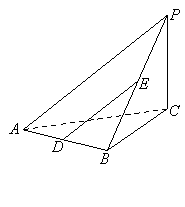
(1)求证：DE∥平面PAC

(2)求证：AB⊥PB

Answer 1

【答案】（1）见解析；（2）见解析.

【解析】(1)证：DE∥PA即可。

（2）PC⊥平面ABC，所以AB⊥PC，因为AB⊥BC，所以AB⊥平面PBC．所以AB⊥PB。

(1)证明：因为D，E分别是AB，PB的中点，

所以DE∥PA．

因为PA平面PAC，且DE平面PAC，

所以DE∥平面PAC．

…………………7分

(2)因为PC⊥平面ABC，且AB平面ABC，

所以AB⊥PC．又因为AB⊥BC，且PC∩BC＝C．

所以AB⊥平面PBC．

又因为PB平面PBC，

所以AB⊥PB． …………………14分