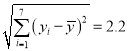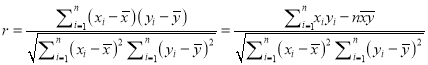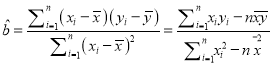题目内容
【题目】已知函数f(x)与函数g(x)的图像关于原点对称,且f(x)=![]() +2x, 若函数F(x)=g(x)-
+2x, 若函数F(x)=g(x)-![]() f(x)+1在区间
f(x)+1在区间![]() 上是增函数,求实数
上是增函数,求实数![]() 的取值范围。
的取值范围。
【答案】(-![]() ,0]
,0]
【解析】
由函数f(x)与函数g(x)的图像关于原点对称,且f(x)=![]() +2x即可求得g(x)=-
+2x即可求得g(x)=-![]() +2x,从而求得:F(x)=-(1+
+2x,从而求得:F(x)=-(1+![]() )
)![]() +2(1-
+2(1-![]() )x+1,对
)x+1,对![]() 的范围分类即可求得使F(x)在区间
的范围分类即可求得使F(x)在区间![]() 上是增函数的实数
上是增函数的实数![]() 的取值范围.
的取值范围.
由题意知,g(x)=-f(-x)=-![]() +2x,则F(x)=-(1+
+2x,则F(x)=-(1+![]() )
)![]() +2(1-
+2(1-![]() )x+1.
)x+1.
当1+![]() =0,即
=0,即![]() =-1时,F(x)=4x+1在区间
=-1时,F(x)=4x+1在区间![]() 上是增函数,从而
上是增函数,从而![]() =-1;
=-1;
当1+![]() 〉0,即
〉0,即![]() 〉-1时,若F(x)在区间
〉-1时,若F(x)在区间![]() 上是增函数,则
上是增函数,则![]() ,解得-1<
,解得-1<![]()
![]() 0;
0;
当1+![]() < 0,即
< 0,即![]() <-1时,若F(x)在区间
<-1时,若F(x)在区间![]() 上是增函数,则
上是增函数,则![]() 显然成立,从而
显然成立,从而![]() <-1;
<-1;
综上所述,实数![]() 的取值范围为(-
的取值范围为(-![]() ,0]。
,0]。

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目