题目内容
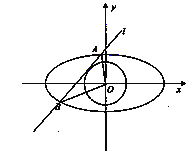
【题目】如图,直线![]() 与圆O:
与圆O: ![]() 且与椭圆C:
且与椭圆C: ![]() 相交于A,B两点
相交于A,B两点
(1)若直线![]() 恰好经过椭圆的左顶点,求弦长AB;
恰好经过椭圆的左顶点,求弦长AB;
(2)设直线OA,OB的斜率分别为k1,k2,判断k1·k2是否为定值,并说明理由
【答案】(1)![]() ;(2)
;(2)![]()
【解析】试题分析:(1)由题意直线![]() 斜率存在,设直线
斜率存在,设直线![]() 因为直线
因为直线![]() 与圆
与圆![]() 相切,所以
相切,所以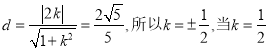 时,
时,  解得
解得![]() ,所以
,所以![]() ,当
,当![]() 时,同理
时,同理![]() (2)ⅰ)当
(2)ⅰ)当![]() 的斜率不存在时,得
的斜率不存在时,得![]() ;ⅱ)当
;ⅱ)当![]() 的斜率存在时,设直线
的斜率存在时,设直线![]()
![]() 因为直线
因为直线![]() 与圆
与圆![]() 相切,
相切, 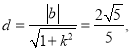 所以
所以![]() ①,
①,![]() 与椭圆进行联立
与椭圆进行联立![]() ,韦达定理所得式子代入可得得
,韦达定理所得式子代入可得得![]() ;
;
试题解析:
(1)由题意直线![]() 斜率存在,设直线
斜率存在,设直线![]() 因为直线
因为直线![]() 与圆
与圆![]() 相切,所以
相切,所以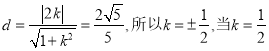 时,
时, 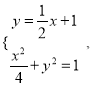 解得
解得![]() ,所以
,所以![]() 当
当![]() 时,同理
时,同理![]() 所以
所以![]()
(2)ⅰ)当![]() 的斜率不存在时,得
的斜率不存在时,得![]() ;
;
ⅱ)当![]() 的斜率存在时,设直线
的斜率存在时,设直线![]()
![]() 因为直线
因为直线![]() 与圆
与圆![]() 相切,
相切, 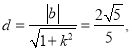 所以
所以![]() ①,
①,![]() ,
,
![]()
![]() ,②
,② ![]() ③,将①②代入③式得
③,将①②代入③式得![]() 所以
所以![]()

练习册系列答案
相关题目