题目内容
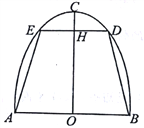
【题目】如图,小明想将短轴长为2,长轴长为4的一个半椭圆形纸片剪成等腰梯形ABDE,且梯形ABDE内接于半椭圆,DE∥AB,AB为短轴,OC为长半轴
(1)求梯形ABDE上底边DE与高OH长的关系式;
(2)若半椭圆上到H的距离最小的点恰好为C点,求底边DE的取值范围
【答案】(1)![]() ;(2)
;(2)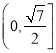
【解析】试题分析:
(1)以![]() 所在直线为
所在直线为![]() 轴,
轴, ![]() 所在直线为
所在直线为![]() 轴,建立直角坐标系,可得半椭圆的方程:
轴,建立直角坐标系,可得半椭圆的方程: ![]() ,设点
,设点![]() ,由
,由![]() 且
且![]() ,可得
,可得![]() 。(2))设半椭圆上一点为
。(2))设半椭圆上一点为![]() 由条件得
由条件得![]() 故
故![]() ,结合对称轴
,结合对称轴![]() 得到
得到![]() ,从而
,从而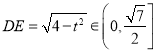 ,即为所求范围。
,即为所求范围。
试题解析:
(1)以![]() 所在直线为
所在直线为![]() 轴,
轴, ![]() 所在直线为
所在直线为![]() 轴,建立直角坐标系
轴,建立直角坐标系
半椭圆的方程: ![]() ,
,
设椭圆上点![]() ,
,
所以![]() 且
且![]() ,
,
所以![]() .
.
(2)设半椭圆上一点为![]()
由题可知点![]()
所以![]() ,
,
又函数![]() 图象的对称轴为
图象的对称轴为![]() ,
,
所以![]()
解得![]()
所以![]()
由(1)知
所以底边DE的取值范围为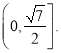

练习册系列答案
 ABC考王全优卷系列答案
ABC考王全优卷系列答案
相关题目