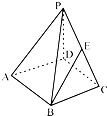
题目内容
【题目】如图,已知椭圆![]() 的离心率为
的离心率为![]() ,过左焦点
,过左焦点![]() 且斜率为
且斜率为![]() 的直线交椭圆
的直线交椭圆![]() 于
于![]() ,
, ![]() 两点,线段
两点,线段![]() 的中点为
的中点为![]() ,直线
,直线![]() 交椭圆
交椭圆![]() 于
于![]() ,
, ![]() 两点.
两点.
(I)求椭圆![]() 的方程.
的方程.
(II)求证:点![]() 在直线
在直线![]() 上.
上.
(III)是否存在实数![]() ,使得
,使得![]() 的面积是
的面积是![]() 面积的
面积的![]() 倍?若存在,求出
倍?若存在,求出![]() 的值.若不存在,说明理由.
的值.若不存在,说明理由.
【答案】(1)![]() (2)见解析(3)
(2)见解析(3)![]()
【解析】试题分析:本题主要考查椭圆的标准方程、直线与椭圆的相交问题、韦达定理、中点坐标公式等基础知识,考查学生的分析问题解决问题的能力、转化能力、计算能力.第一问,利用已知的离心率和左焦点坐标,得到基本量a,b,c的值,从而得到椭圆的标准方程;第二问,设出点A、B、M的坐标和直线的方程,令直线的方程与椭圆的方程联立,利用所得方程,根据韦达定理得到![]() ,从而得到
,从而得到![]() 的坐标,
的坐标, ![]() 由直线方程获得,验证
由直线方程获得,验证![]() 是否在
是否在![]() 上即可;第三问,数形结合,根据已知条件将题目转化为C点坐标
上即可;第三问,数形结合,根据已知条件将题目转化为C点坐标![]() 与M点坐标
与M点坐标![]() 的关系,通过直线与椭圆联立消参,得到
的关系,通过直线与椭圆联立消参,得到![]() 的坐标,令
的坐标,令![]() ,解出k的值,k有解,即存在.
,解出k的值,k有解,即存在.
试题解析:(1)由题意可知![]() ,
, ![]() ,于是
,于是![]() .
.
所以,椭圆的标准方程为![]() 程. 3分
程. 3分
(2)设![]() ,
, ![]() ,
, ![]() ,
,
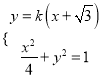 即
即![]() .
.
所以, ![]() ,
, ![]() ,
, ![]() ,
,
于是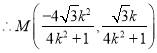 .
.
因为![]() ,所以
,所以![]() 在直线
在直线![]() 上. 8分
上. 8分
(3)由(2)知点A到直线CD的距离与点B到直线CD的距离相等,
若BDM的面积是ACM面积的3倍,
则|DM|=3|CM|,因为|OD|=|OC|,于是M为OC中点,;
设点C的坐标为![]() ,则
,则![]() .因为
.因为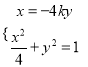 ,解得
,解得![]() .
.
于是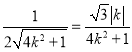 ,解得
,解得![]() ,所以
,所以![]() . 14分
. 14分

【题目】某单位有车牌尾号为![]() 的汽车
的汽车![]() 和尾号为
和尾号为![]() 的汽车
的汽车![]() ,两车分属于两个独立业务部分.对一段时间内两辆汽车的用车记录进行统计,在非限行日,
,两车分属于两个独立业务部分.对一段时间内两辆汽车的用车记录进行统计,在非限行日, ![]() 车日出车频率
车日出车频率![]() ,
, ![]() 车日出车频率
车日出车频率![]() .该地区汽车限行规定如下:
.该地区汽车限行规定如下:
车尾号 |
|
|
|
|
|
限行日 | 星期一 | 星期二 | 星期三 | 星期四 | 星期五 |
现将汽车日出车频率理解为日出车概率,且![]() ,
, ![]() 两车出车相互独立.
两车出车相互独立.
(I)求该单位在星期一恰好出车一台的概率.
(II)设![]() 表示该单位在星期一与星期二两天的出车台数之和,求
表示该单位在星期一与星期二两天的出车台数之和,求![]() 的分布列及其数学期望
的分布列及其数学期望![]() .
.