题目内容
【题目】如图1,平面四边形![]() 中,
中,![]() 为
为![]() 上一点,
上一点,![]() 和
和![]() 均为等边三角形,
均为等边三角形,![]()
![]() 分别是
分别是![]() 和
和![]() 的中点,将四边形
的中点,将四边形![]() 沿
沿![]() 向上翻折至四边形
向上翻折至四边形![]() 的位置,使二面角
的位置,使二面角![]() 为直二面角,如图2所示.
为直二面角,如图2所示.
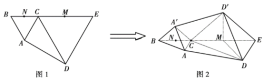
(1)求证:![]() 平面
平面![]() ;
;
(2)求平面![]() 与平面
与平面![]() 所成角的正弦值.
所成角的正弦值.
【答案】(1)证明见解析;(2)![]() .
.
【解析】
(1)推导出![]() ,
,![]() ,从而直线
,从而直线![]() 平面
平面![]() ,进而直线
,进而直线![]() 平面
平面![]() ,同理可证直线
,同理可证直线![]() 平面
平面![]() ,由此能证明平面
,由此能证明平面![]() 平面
平面![]() ,从而有
,从而有![]() 平面
平面![]() ;(2)以
;(2)以![]() 为坐标原点,
为坐标原点,![]() ,
,![]() ,
,![]() 所在直线分别为
所在直线分别为![]() ,
,![]() ,
,![]() 轴,建立空间直角坐标系
轴,建立空间直角坐标系![]() ,利用向量法能求出平面
,利用向量法能求出平面![]() 与平面
与平面![]() 所成角的正弦值.
所成角的正弦值.
(1)在等边△![]() 和
和![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,
所以直线![]() 平面
平面![]() ,即直线
,即直线![]() 平面
平面![]() ,
,
同理可证直线![]() 平面
平面![]() ,
,
故平面![]() 平面
平面![]() ,
,
又![]() 平面
平面![]() ,从而有
,从而有![]() 平面
平面![]() .
.
(2)如图,以![]() 为坐标原点,
为坐标原点,![]() ,
,![]() ,
,![]() 所在直线分别为
所在直线分别为![]() ,
,![]() ,
,![]() 轴,
轴,
建立空间直角坐标系![]() ,
,
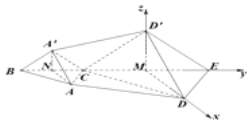
![]() ,0,
,0,![]() ,
,![]() ,1,
,1,![]() ,
,![]() ,
,![]() ,
,
![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .
.
![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,
设平面![]() 的一个法向量为
的一个法向量为![]() ,
,![]() ,
,![]() ,
,
由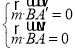 ,得
,得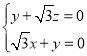 ,令
,令![]() ,得
,得![]() ,
,
所以平面![]() 的一个法向量为
的一个法向量为![]() ,
,
同理,设平面![]() 的一个法向量为
的一个法向量为![]() ,
,
由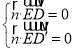 ,得
,得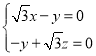 ,
,
令![]() ,得
,得![]() ,所以平面
,所以平面![]() 的一个法向量为
的一个法向量为![]() ,
,![]() ,
,![]() .
.
从而![]() ,
,
故平面![]() 与平面
与平面![]() 所成角的正弦值为
所成角的正弦值为![]() .
.

【题目】某公司A产品生产的投入成本x(单位:万元)与产品销售收入y(单位:十万元)存在较好的线性关系,下表记录了该公司最近8次该产品的相关数据,且根据这8组数据计算得到y关于x的线性回归方程为![]() .
.
x(万元) | 6 | 7 | 8 | 11 | 12 | 14 | 17 | 21 |
y(十万元) | 1.2 | 1.5 | 1.7 | 2 | 2.2 | 2.4 | 2.6 | 2.9 |
(1)求![]() 的值(结果精确到0.0001),并估计公司A产品投入成本30万元后产品的销售收入(单位:十万元).
的值(结果精确到0.0001),并估计公司A产品投入成本30万元后产品的销售收入(单位:十万元).
(2)该公司B产品生产的投入成本u(单位:万元)与产品销售收入v(单位:十万元)也存在较好的线性关系,且v关于u的线性回归方程为![]() .
.
(i)估计该公司B产品投入成本30万元后的毛利率(毛利率![]() );
);
(ii)判断该公司A,B两个产品都投入成本30万元后,哪个产品的毛利率更大.
