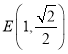题目内容
【题目】已知曲线![]() 的参数方程为:
的参数方程为:![]() (
(![]() 为参数),
为参数),![]() 的参数方程为:
的参数方程为:![]() (
(![]() 为参数).
为参数).
(1)化![]() 、
、![]() 的参数方程为普通方程,并说明它们分别表示什么曲线;
的参数方程为普通方程,并说明它们分别表示什么曲线;
(2)若直线![]() 的极坐标方程为:
的极坐标方程为:![]() ,曲线
,曲线![]() 上的点
上的点![]() 对应的参数
对应的参数![]() ,曲线
,曲线![]() 上的点
上的点![]() 对应的参数
对应的参数![]() ,求
,求![]() 的中点
的中点![]() 到直线
到直线![]() 的距离.
的距离.
【答案】(1) ![]() :
:![]() ;
;![]() :
:![]() ;
;![]() 以圆心为
以圆心为![]() ,半径为1的圆,
,半径为1的圆,![]() 以坐标原点为中心,焦点在
以坐标原点为中心,焦点在![]() 轴的椭圆;(2)
轴的椭圆;(2)![]()
【解析】
(1)直接利用参数方程组消去参数即可得到它们的普通方程;
(2)根据已知条件分别求出![]() 、
、![]() 两点坐标以及
两点坐标以及![]() 点坐标,再利用点到直线的距离公式即可求出.
点坐标,再利用点到直线的距离公式即可求出.
(1)曲线![]() 的参数方程为:
的参数方程为:![]() (
(![]() 为参数),
为参数),
即![]() ,且
,且![]() ,则
,则
![]() :
:![]() ;
;
![]() 的参数方程为:
的参数方程为:![]() (
(![]() 为参数),
为参数),
即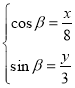 ,且
,且![]() ,则
,则
![]() :
:![]() ;
;
![]() 以圆心为
以圆心为![]() ,半径为1的圆,
,半径为1的圆,
![]() 以坐标原点为中心,焦点在
以坐标原点为中心,焦点在![]() 轴的椭圆;
轴的椭圆;
(2)曲线![]() 上的点
上的点![]() 对应的参数
对应的参数![]() ,
,
所以![]() ,
,
曲线![]() 上的点
上的点![]() 对应的参数
对应的参数![]() ,
,
所以![]() ,
,
所以![]() 的中点
的中点![]() 的坐标为
的坐标为![]() ,
,
因为直线![]() 的极坐标方程为:
的极坐标方程为:![]() ,
,
即直线![]() 的普通方程为:
的普通方程为:![]() ,
,
所以![]() 的中点
的中点![]() 到直线
到直线![]() 的距离
的距离![]()

练习册系列答案
相关题目
【题目】已知某校6个学生的数学和物理成绩如下表:
学生的编号 | 1 | 2 | 3 | 4 | 5 | 6 |
数学 | 89 | 87 | 79 | 81 | 78 | 90 |
物理 | 79 | 75 | 77 | 73 | 72 | 74 |
(1)若在本次考试中,规定数学在80分以上(包括80分)且物理在75分以上(包括75分)的学生为理科小能手.从这6个学生中抽出2个学生,设![]() 表示理科小能手的人数,求
表示理科小能手的人数,求![]() 的分布列和数学期望;
的分布列和数学期望;
(2)通过大量事实证明发现,一个学生的数学成绩和物理成绩具有很强的线性相关关系,在上述表格是正确的前提下,用![]() 表示数学成绩,用
表示数学成绩,用![]() 表示物理成绩,求
表示物理成绩,求![]() 与
与![]() 的回归方程.
的回归方程.
参考数据和公式:![]() ,其中
,其中 ,
,![]() .
.