题目内容
若集合A={x|x2-2x-8=0},B={x|ax-6=0}
(1)若B=∅,求实数a的值;
(2)若A∪B=A,求实数a组成的集合C.
(1)若B=∅,求实数a的值;
(2)若A∪B=A,求实数a组成的集合C.
(1)∵B={x|ax-6=0}=Φ,
∴方程ax-6=0无解,
∴a=0,即a的值是0;
(2)∵A={x|x2-2x-8=0}={x|x=-2或x=4}={-2,4},
且A∪B=A,
∴B=Φ,B={-2},B={4}或B={-2,4};
当B=Φ时,由(1)知a=0;
当B={-2}时,方程ax-6=0的解是x=-2,∴a=-3;
当B={4}时,方程ax-6=0的解是x=4,∴a=
;
当B={-2,4}时,方程ax-6=0的解是x=-2或x=4,显然不成立;
∴由实数a组成的集合为C={0,
,-3}.
∴方程ax-6=0无解,
∴a=0,即a的值是0;
(2)∵A={x|x2-2x-8=0}={x|x=-2或x=4}={-2,4},
且A∪B=A,
∴B=Φ,B={-2},B={4}或B={-2,4};
当B=Φ时,由(1)知a=0;
当B={-2}时,方程ax-6=0的解是x=-2,∴a=-3;
当B={4}时,方程ax-6=0的解是x=4,∴a=
| 3 |
| 2 |
当B={-2,4}时,方程ax-6=0的解是x=-2或x=4,显然不成立;
∴由实数a组成的集合为C={0,
| 3 |
| 2 |

练习册系列答案
相关题目
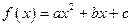 .(1)若
.(1)若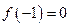 ,试判断函数
,试判断函数 零点个数;(2)若对
零点个数;(2)若对 且
且 ,
,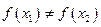 ,试证明
,试证明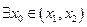 ,使
,使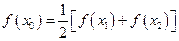 成立。(3)是否存在
成立。(3)是否存在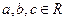 ,使
,使 同时满足以下条件①对
同时满足以下条件①对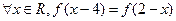 ,且
,且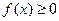 ;②对
;②对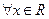 ,都有
,都有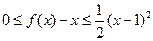 。若存在,求出
。若存在,求出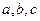 的值,若不存在,请说明理由。
的值,若不存在,请说明理由。