题目内容
某工厂有 名工人,现接受了生产
名工人,现接受了生产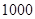 台
台 型高科技产品的总任务.已知每台
型高科技产品的总任务.已知每台 型产品由
型产品由 个
个 型装置和
型装置和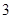 个
个 型装置配套组成,每个工人每小时能加工
型装置配套组成,每个工人每小时能加工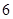 个
个 型装置或
型装置或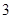 个
个 型装置.现将工人分成两组同时开始加工,每组分别加工一种装置(完成自己的任务后不再支援另一组).设加工
型装置.现将工人分成两组同时开始加工,每组分别加工一种装置(完成自己的任务后不再支援另一组).设加工 型装置的工人有
型装置的工人有 人,他们加工完
人,他们加工完 型装置所需时间为
型装置所需时间为 ,其余工人加工完
,其余工人加工完 型装置所需时间为
型装置所需时间为 (单位:小时,可不为整数).
(单位:小时,可不为整数).
(1)写出 、
、 的解析式;
的解析式;
(2)写出这 名工人完成总任务的时间
名工人完成总任务的时间 的解析式;
的解析式;
(3)应怎样分组,才能使完成总任务用的时间最少?
(1) ,
, (
( ,
, );
);
(2) ;
;
(3)加工 型装置,
型装置, 型装置的人数分别为
型装置的人数分别为 、
、 或
或 、
、 .
.
解析试题分析:(1)根据定义求出函数 与
与 的解析式,并求出函数的定义域;(2)对两个函数
的解析式,并求出函数的定义域;(2)对两个函数 与
与 作差,比较
作差,比较 与
与 的大小,根据相应的
的大小,根据相应的 的取值范围确定
的取值范围确定 的解析式;(3)考查函数
的解析式;(3)考查函数 在每段定义域上的单调性,并求出函数
在每段定义域上的单调性,并求出函数 相应的最小值,从而确定加工两种不同的零件的人数.
相应的最小值,从而确定加工两种不同的零件的人数.
试题解析:(1)由题意知,需加工 型装置4000个,加工
型装置4000个,加工 型装置3000个,所用工人分别为
型装置3000个,所用工人分别为 人和(
人和( )
)
人,∴ ,
, ,
,
即 ,
, (
( ,
, ) 4分
) 4分
(2)

 ,
,
∵ ,∴
,∴ ,
,
当 时,
时, ,
, ,
, ,
,
当 时,
时, ,
, ,
, ,
, 9分
9分
(3)完成总任务所用时间最少即求 的最小值,
的最小值,
当 时,
时, 递减,∴
递减,∴
 ,
,
∴ ,此时
,此时 , 11分
, 11分
当 时,
时, 递增,∴
递增,∴
 ,
,
∴ ,此时
,此时 , 13分
, 13分
∴ ,
,
∴加工G型装置,H型装置的人数分别为86、130或87、129. 14分
考点:1.分段函数;2.分段函数的单调性与最值

练习册系列答案
 学期复习一本通学习总动员期末加暑假延边人民出版社系列答案
学期复习一本通学习总动员期末加暑假延边人民出版社系列答案 芒果教辅暑假天地重庆出版社系列答案
芒果教辅暑假天地重庆出版社系列答案
相关题目
 构成的:对于定义域内任意两个不相等的实数
构成的:对于定义域内任意两个不相等的实数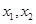 ,都有
,都有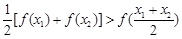 .
.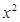 及
及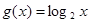 是否在集合A中,并说明理由;
是否在集合A中,并说明理由; ,试写出一个满足以上条件的函数
,试写出一个满足以上条件的函数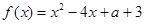 ,
,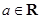 .
. 在
在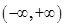 上至少有一个零点,求
上至少有一个零点,求 的取值范围;
的取值范围;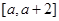 上的最大值为
上的最大值为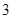 ,求
,求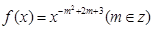 为偶函数,且在区间
为偶函数,且在区间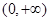 上是单调增函数
上是单调增函数 的解析式;
的解析式;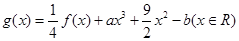 ,其中
,其中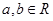 .若函数
.若函数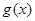 仅在
仅在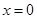 处有极值,求
处有极值,求 的取值范围.
的取值范围.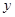 (升)关于行驶速度
(升)关于行驶速度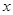 (千米/每小时)的函数解析式可以表示为
(千米/每小时)的函数解析式可以表示为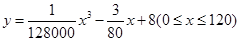 ,已知甲、乙两地相距100千米.
,已知甲、乙两地相距100千米.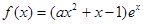 ,其中
,其中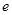 是自然对数的底数,
是自然对数的底数,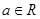 .
.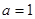 ,求曲线
,求曲线 在点
在点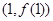 处的切线方程;
处的切线方程;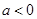 ,求
,求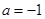 ,函数
,函数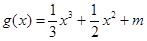 的图象有3个不同的交点,求实数
的图象有3个不同的交点,求实数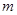 的取值范围.
的取值范围. 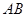 长为2m,跳水板距水面
长为2m,跳水板距水面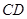 的高
的高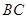 为3m,
为3m, =5m,
=5m,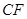 =6m,为安全和空中姿态优美,训练时跳水曲线应在离起跳点
=6m,为安全和空中姿态优美,训练时跳水曲线应在离起跳点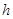 m(
m(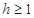 )时达到距水面最大高度4m,规定:以
)时达到距水面最大高度4m,规定:以 为纵轴建立直角坐标系.
为纵轴建立直角坐标系.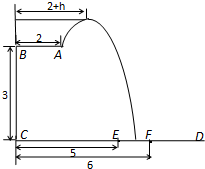
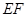 内入水时才能达到压水花的训练要求,求达到压水花的训练要求时
内入水时才能达到压水花的训练要求,求达到压水花的训练要求时 ,
,
 .
. 的解集;
的解集; 的不等式
的不等式 在
在 的取值范围.
的取值范围.