题目内容
把长为10cm的细铁丝截成两段,各自围成一个正方形,求这两个正方形面积之和的最小值。
解析试题分析:设出其中一段的长为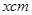 ,表示出另一段的长,从而得正方形面积表示式为二次函数即可求解,
,表示出另一段的长,从而得正方形面积表示式为二次函数即可求解,
但要注意自变量得取值范围,即函数定义域。
试题解析:设铁丝一段长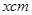 ,
,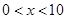 ,两正方形面积之和为
,两正方形面积之和为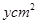 , 3分
, 3分
则另一段铁丝长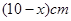 , 5分
, 5分
依题意,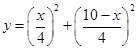
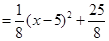 , 10分
, 10分
当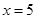 时,取最大值
时,取最大值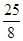 . 13分
. 13分
答:(略) 14分
考点:二次函数最值.

练习册系列答案
 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案
相关题目
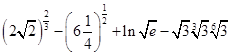
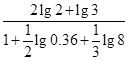
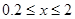 时,排水量V是垃圾杂物密度x的一次函数。
时,排水量V是垃圾杂物密度x的一次函数。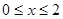 时,求函数V(x)的表达式;
时,求函数V(x)的表达式; 可以达到最大,求出这个最大值。
可以达到最大,求出这个最大值。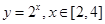 的值域为集合
的值域为集合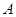 ,
, 的定义域为集合
的定义域为集合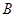 ,其中
,其中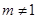 。(1)当
。(1)当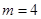 ,求
,求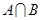 ;(2)设全集为R,若
;(2)设全集为R,若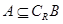 ,求实数
,求实数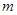 的取值范围.
的取值范围. 千件,并且全部销售完,每千件的销售收入为
千件,并且全部销售完,每千件的销售收入为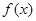 万元,且
万元,且
 (万元)关于年产品
(万元)关于年产品 为偶函数,且在区间
为偶函数,且在区间 上是单调增函数
上是单调增函数 的解析式;
的解析式; ,其中
,其中 .若函数
.若函数 仅在
仅在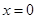 处有极值,求
处有极值,求 的取值范围.
的取值范围. 名工人,现接受了生产
名工人,现接受了生产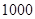 台
台 型高科技产品的总任务.已知每台
型高科技产品的总任务.已知每台 个
个 型装置和
型装置和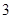 个
个 型装置配套组成,每个工人每小时能加工
型装置配套组成,每个工人每小时能加工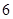 个
个 人,他们加工完
人,他们加工完 ,其余工人加工完
,其余工人加工完 (单位:小时,可不为整数).
(单位:小时,可不为整数). 的解析式;
的解析式; 满足对任意实数
满足对任意实数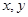 都有
都有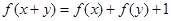 成立,且当
成立,且当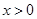 时,
时,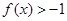 ,
,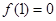 .
.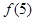 的值;
的值;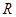 上的单调性,并证明;
上的单调性,并证明;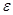 ,总能找到一个正实数
,总能找到一个正实数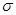 ,使得当
,使得当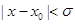 时,
时,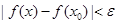 ,则称函数
,则称函数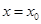 处连续。试证明:
处连续。试证明: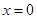 处连续.
处连续. 有最小正周期4,且
有最小正周期4,且 时,
时, 。
。 上的解析式;
上的解析式; 上的单调性,并给予证明;
上的单调性,并给予证明; 为何值时,关于方程
为何值时,关于方程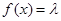 在
在