题目内容
11.函数f(x)=ln(3-2x)+$\sqrt{x+2}$的定义域为$[{-2,\frac{3}{2}})$.分析 根据函数成立的条件即可求函数的定义域.
解答 解:要使函数有意义,则$\left\{\begin{array}{l}{3-2x>0}\\{x+2≥0}\end{array}\right.$,
即$\left\{\begin{array}{l}{x<\frac{3}{2}}\\{x≥-2}\end{array}\right.$,即-2≤x<$\frac{3}{2}$,
即函数的定义域为$[{-2,\frac{3}{2}})$,
故答案为:$[{-2,\frac{3}{2}})$
点评 本题主要考查函数的定义域的求解,要求熟练掌握常见函数成立的条件.

练习册系列答案
相关题目
2.若命题p的逆命题是q,命题p的逆否命题是r,则q与r的关系是( )
| A. | 互为逆否命题 | B. | 互为逆命题 | C. | 互为否命题 | D. | 不能确定 |
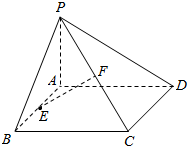 如图,已知矩形ABCD所在平面外一点P,PA⊥平面ABCD,E,F分别是AB,PC的中点,AB=$\frac{1}{2}$AD=1.
如图,已知矩形ABCD所在平面外一点P,PA⊥平面ABCD,E,F分别是AB,PC的中点,AB=$\frac{1}{2}$AD=1.