题目内容
16.(1)求200310除以8的余数;(2)求1.9975精确到0.001的近似值.
分析 (1)先将幂利用二项式表示,使其底数用8的倍数表示,利用二项式定理展开得到余数;
(2)将1.997写出2-0.003;利用二项式定理展开,结合精确度,可求出近似值
解答 解:(1)200310=(2000+3)10
=C100•200010+C101•20009•3+C102•20008•32+…+C109•20001•39+C1010310
∵(C100•200010+C101•20009•3+C102•20008•32+…+C109•20001•39)为2000的倍数,
故∵(C100•200010+C101•20009•3+C102•20008•32+…+C109•20001•39)为8的倍数,
故200310除以8的余数等于310除以8的余数,
又∵310=95=(8+1)5=C50•85+C51•84+C52•83+C53•82+C54•8+1,
(C50•85+C51•84+C52•83+C53•82+C54•8)为8的倍数,
故200310除以8的余数为1;
(2)解:1.9975=(2-0.003)5=C5025-C51•24•(0.003)1+C52•23•(0.003)2-C53•22•(0.003)3+C54•2•(0.003)4-C55•(0.003)5≈32-5×16•(-0.003)=31.760
点评 本题考查利用二项式定理的展开式解决整除性问题.关键是将幂形式写成二项式形式

练习册系列答案
相关题目
4.已知命题P:存在x∈R,x3=1-x2;命题q:△ABC中,“A>B”是“sinA>sinB”的充分条件;则下列命题是真命题的是( )
| A. | p且q | B. | p或?q | C. | ?p且?q | D. | ?p或q |
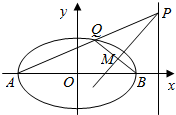 椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的左、右顶点为A、B,点P在直线x=t(t为常数)上,线段AP与椭圆C交于点Q(异于点A),设以PQ为直径的圆交直线BQ于点M(异于点Q),问直线PM是否恒过一个定点?
椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的左、右顶点为A、B,点P在直线x=t(t为常数)上,线段AP与椭圆C交于点Q(异于点A),设以PQ为直径的圆交直线BQ于点M(异于点Q),问直线PM是否恒过一个定点?