题目内容
1.已知m是常数,对任意实数x,不等式|3x+1|+|2-3x|≥m恒成立(1)求m的最大值;
(2)设a>b>0,求证:a+$\frac{4}{{a}^{2}-2ab+{b}^{2}}$≥b+m.
分析 (1)利用恒成立问题,只要求出|3x+1|+|2-3x|的最小值即可;
(2)对式子变形,利用基本不等式求a+$\frac{4}{{a}^{2}-2ab+{b}^{2}}$最小值即可.
解答 (1)解:对任意实数x,不等式|3x+1|+|2-3x|≥m恒成立,所以|x+$\frac{1}{3}$|+|x-$\frac{2}{3}$|min=1≥$\frac{m}{3}$恒成立,所以m≤3,所以m的最大值为3;
(2)证明:a>b>0,a-b+$\frac{4}{{a}^{2}-2ab+{b}^{2}}$=$\frac{a-b}{2}+\frac{a-b}{2}+\frac{4}{(a-b)^{2}}≥$3$\root{3}{\frac{a-b}{2}•\frac{a-b}{2}•\frac{4}{(a-b)^{2}}}$=3,
所以a-b+$\frac{4}{{a}^{2}-2ab+{b}^{2}}$≥m,即a+$\frac{4}{{a}^{2}-2ab+{b}^{2}}$≥b+m.
点评 本题考查了不等式的恒成立问题以及利用基本不等式证明不等式,考查了学生分析问题、解决问题的能力,属于中档题.

练习册系列答案
 优生乐园系列答案
优生乐园系列答案
相关题目
9.已知P(2,4)在双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1({a>0,b>0})$的渐近线上,则该双曲线的离心率为( )
| A. | $\sqrt{5}$ | B. | 2 | C. | $\sqrt{3}$ | D. | $\sqrt{2}$ |
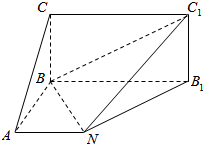 如图,矩形BB1C1C所在平面与底面ANB1B垂直,在直角梯形ANB1B中,AB⊥AN,CB=BA=AN=4,BB1=8,AN∥BB1.
如图,矩形BB1C1C所在平面与底面ANB1B垂直,在直角梯形ANB1B中,AB⊥AN,CB=BA=AN=4,BB1=8,AN∥BB1.