题目内容
【题目】已知函数f(x)=ax+lnx(a∈R),g(x)=x2emx(m∈R,e为自然对数的底数).
(1)讨论函数f(x)的单调性及最值;
(2)若a>0,且对x1,x2∈[0,2],f(x1+1)≥g(x2)+a﹣1恒成立,求实数m的取值范围.
【答案】(1)见解析;(2)(﹣∞,﹣ln2]
【解析】
(1)![]() .对
.对![]() 分类讨论,利用导数研究函数的单调性极值与最值,即可得出;(2)原命题等价于
分类讨论,利用导数研究函数的单调性极值与最值,即可得出;(2)原命题等价于![]() ,且对
,且对![]() ,
,![]() ,
,![]() 恒成立.由(1)可知:当
恒成立.由(1)可知:当![]() 时,函数
时,函数![]() 在
在![]() 单调递增,故
单调递增,故![]() 在
在![]() ,
,![]() 上单调递增,可得
上单调递增,可得![]() (1)
(1)![]() .对
.对![]() ,
,![]() ,
,![]() 恒成立
恒成立![]() 对
对![]() ,
,![]() ,
,![]() 恒成立.对
恒成立.对![]() 分类讨论:利用导数研究函数的单调性极值与最值,即可得出.
分类讨论:利用导数研究函数的单调性极值与最值,即可得出.
(1)![]() =a+
=a+![]() (x∈(0,+∞)).
(x∈(0,+∞)).
当a≥0时,![]() ≥0,
≥0,
∴f(x)在x∈(0,+∞)单调递增,无最值.
当a<0时,![]()
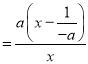 (x∈(0,+∞)).
(x∈(0,+∞)).
可得函数f(x)在(0,![]() )上单调递增,在(
)上单调递增,在(![]() ,+∞)上单调递减.
,+∞)上单调递减.
当x=![]() 时,函数f(x)取得极小值即最小值,且最大值为f(
时,函数f(x)取得极小值即最小值,且最大值为f(![]() )=﹣1﹣ln(﹣a),无最大值.
)=﹣1﹣ln(﹣a),无最大值.
(2)a>0,且对x1,x2∈[0,2],f(x1+1)≥g(x2)+a﹣1恒成立,等价于a>0,且对x∈[0,2],f(x+1)min≥g(x)max+a﹣1恒成立.
由(1)可知:当a>0时,函数f(x)在x∈(0,+∞)单调递增,故y=f(x+1)在x∈[0,2]上单调递增,
∵x∈[0,2],∴(x+1)∈[1,3],故f(x+1)min=f(1)=a.
∴对x∈[0,2],f(x+1)min≥g(x)max+a﹣1恒成立对x∈[0,2],g(x)max≤1恒成立.
对m分类讨论:m=0时,g(x)=x2,x=0,函数g(x)取得最大值,g(2)=4,不满足g(x)max≤1.
当m≠0时,![]() =2xemx+mx2emx=xemx(mx+2).令
=2xemx+mx2emx=xemx(mx+2).令![]() =0,解得x=0,x=﹣
=0,解得x=0,x=﹣![]() .
.
①当﹣![]() ≥2,即﹣1≤m<0时,对x∈[0,2],
≥2,即﹣1≤m<0时,对x∈[0,2],![]() ≥0,因此g(x)在此区间上单调递增.∴g(x)max=g(2)=4e2m.
≥0,因此g(x)在此区间上单调递增.∴g(x)max=g(2)=4e2m.
由4e2m≤1,解得m≤﹣ln2.∴﹣1≤m≤﹣ln2.
②当2>﹣![]() >0,即m<﹣1时,可得函数g(x)在x∈[0,﹣
>0,即m<﹣1时,可得函数g(x)在x∈[0,﹣![]() )上单调递增,在(﹣
)上单调递增,在(﹣![]() ,2]上单调递减.
,2]上单调递减.
∴g(x)max=g(﹣![]() )=
)=![]() e﹣2.由
e﹣2.由![]() e﹣2≤1,解得m≤﹣
e﹣2≤1,解得m≤﹣![]() .∴m<﹣1.
.∴m<﹣1.
③当﹣![]() ≤0,即m>0时,对x∈[0,2],
≤0,即m>0时,对x∈[0,2],![]() ≥0,因此g(x)在此区间上单调递增.∴g(x)max=g(2)=4e2m.
≥0,因此g(x)在此区间上单调递增.∴g(x)max=g(2)=4e2m.
此时4e2m≤1,不成立,舍去.
综上可得:实数m的取值范围是(﹣∞,﹣ln2].

 阅读快车系列答案
阅读快车系列答案