题目内容
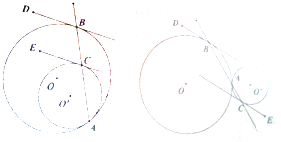已知：如图，⊙O和⊙O′相切于点A，直线AB和⊙O的另一个交点为B，和⊙O′的另一个交点为C，BD，CE分别切⊙O′，⊙O于点B，C．求证：BD∥CE．研究：两圆外切时结论还成立吗？考点：与圆有关的比例线段
专题：选作题,立体几何
分析：利用切割线定理，即可证明结论．
解答：
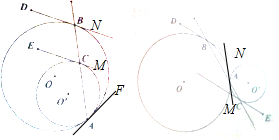解：设两圆的切线为AF，则∠MCA=∠A，∠NBC=∠A，
∴∠MCA=∠NBC，
∴BD∥CE；
圆外切时结论还成立．
证明如下：设两圆的切线为MN，则∠MCA=∠MAC，∠NBA=∠NAB，
∴∠MCA=∠NBA，
∴BD∥CE．
解：设两圆的切线为AF，则∠MCA=∠A，∠NBC=∠A，∴∠MCA=∠NBC，
∴BD∥CE；
圆外切时结论还成立．
证明如下：设两圆的切线为MN，则∠MCA=∠MAC，∠NBA=∠NAB，
∴∠MCA=∠NBA，
∴BD∥CE．
点评：本题考查与圆有关的比例线段，考查切割线定理，考查学生分析解决问题的能力，比较基础．
练习册系列答案
相关题目
“x=-2”是“x≠0”的（ ）
| A、充分而不必要条件 |
| B、必要而不充分条件 |
| C、充分必要条件 |
| D、既不充分也不必要条件 |
在△ABC中，D是BC边上的一点，
=λ（
+
）．|
|=2，|
=4，若记
=
，
=
，则用
，
表示
所得的结果为（ ）
| AD |
| ||
|
|
| ||
|
|
| AB |
| AC| |
| AB |
| a |
| AC |
| b |
| a |
| b |
| BD |
A、
| ||||||||
B、
| ||||||||
C、-
| ||||||||
D、
|
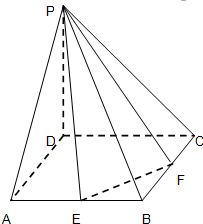已知正方形ABCD，边长为1，过D作PD⊥平面ABCD，且PD=2，E，F分别是AB和BC的中点．