题目内容
过点A(1,2)作圆x2+y2+2x-4y-164=0的弦,其中弦长为整数的共有 条.
考点:直线与圆的位置关系
专题:直线与圆
分析:化简圆的方程为标准方程,求出弦长的最小值和最大值,取其整数个数.
解答:
解:将圆的方程化为标准方程得:(x+1)2+(y-2)2=169,
∴圆心坐标为(-1,2),半径r=13,
∵A到圆心的距离d=
=
=2,
∴最短的弦长为2
=2
=2
≈25.7,最长的弦长为26,
则圆心(-1,2),半径r=13过点A(11,2)的最短的弦长为26,最长的弦长为26,
则共有弦长为整数只有1条.
故答案为:1
∴圆心坐标为(-1,2),半径r=13,
∵A到圆心的距离d=
| (-1-1)2+(2-2)2 |
| 4 |
∴最短的弦长为2
| r2-d2 |
| 169-4 |
| 165 |
则圆心(-1,2),半径r=13过点A(11,2)的最短的弦长为26,最长的弦长为26,
则共有弦长为整数只有1条.
故答案为:1
点评:此题考查了直线与圆相交的性质,实际上是求弦长问题.

练习册系列答案
 小学课时特训系列答案
小学课时特训系列答案
相关题目
已知直线l1:3ax+(a2-1)y+6=0与l2:x+(a-1)y=0平行,则实数a的取值为( )
A、.1或-
| ||
B、
| ||
| C、1 | ||
D、
|
函数y=
sinx+cosx的一个单调递减区间是( )
| 3 |
A、[-
| ||||
| B、[-π,0] | ||||
C、[-
| ||||
D、[
|
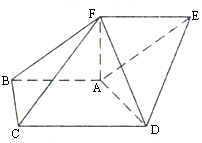 在五面体ABCDEF中,AB∥DC,∠BAD=
在五面体ABCDEF中,AB∥DC,∠BAD=