题目内容
【题目】已知函数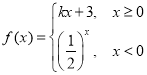 若方程
若方程![]() 恰有三个实数根,则实数
恰有三个实数根,则实数![]() 的取值范围是_______.
的取值范围是_______.
【答案】![]()
【解析】
令f(t)=2,解出t,则f(x)=t,讨论k的符号,根据f(x)的函数图象得出t的范围即可.
解:令f(t)=2得t=﹣1或t![]() (k≠0).
(k≠0).
∵f(f(x))﹣2=0,∴f(f(x))=2,
∴f(x)=﹣1或f(x)![]() (k≠0).
(k≠0).
(1)当k=0时,做出f(x)的函数图象如图所示:
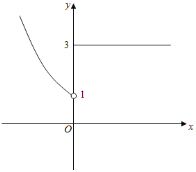
由图象可知f(x)=﹣1无解,即f(f(x))﹣2=0无解,不符合题意;
(2)当k>0时,做出f(x)的函数图象如图所示:
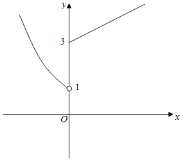
由图象可知f(x)=﹣1无解,f(x)![]() 无解,即f(f(x))﹣2=0无解,不符合题意;
无解,即f(f(x))﹣2=0无解,不符合题意;
(3)当k<0时,做出f(x)的函数图象如图所示:
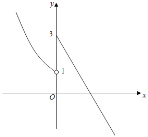
由图象可知f(x)=﹣1有1解,
∵f(f(x))﹣2=0有3解,∴f(x)![]() 有2解,
有2解,
∴1![]() ,解得﹣1<k
,解得﹣1<k![]() .
.
综上,k的取值范围是(﹣1,![]() ].
].
故答案为:(﹣1,![]() ]
]

练习册系列答案
相关题目