题目内容
（本小题满分10分）已知二次函数f(x)满足：①在x=1时有极值；②图象过点(0,-3)，且在该点处的切线与直线2x+y=0平行．
⑴求f(x)的解析式；
⑵求函数g(x)=f(x2)的单调递增区间.
⑴求f(x)的解析式；
⑵求函数g(x)=f(x2)的单调递增区间.
解：⑴设f(x)=ax2+bx+c，则f ¢(x)=2ax+b．
由题设可得：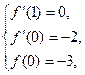
即
解得
所以f(x)=x2-2x-3．
⑵g(x)=f(x2)=x4－2x2－3，g¢(x)=4x3－4x=4x(x－1)(x+1)．列表：
由表可得：函数g(x)的单调递增区间为(-1,0)，(1,+∞)．
由题设可得：
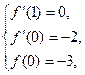即解得所以f(x)=x2-2x-3．
⑵g(x)=f(x2)=x4－2x2－3，g¢(x)=4x3－4x=4x(x－1)(x+1)．列表：
| x | (-∞,-1) | -1 | (-1,0) | 0 | (0,1) | 1 | (1,+∞) |
| f¢(x) | － | 0 | + | 0 | － | 0 | + |
| f(x) | ↘ | | ↗ | | ↘ | | ↗ |
由表可得：函数g(x)的单调递增区间为(-1,0)，(1,+∞)．
略
练习册系列答案
阅读快车系列答案
相关题目
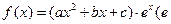为自然对数的底，
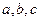为常数），若函数
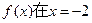处取得极值，且
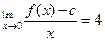.（1）求实数
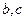的值；（2）若函数
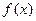在区间[1，2]上是增函数，求实数
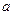的取值范围。
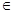R，若关于的不等式
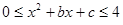的解集为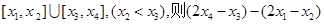
的最小值是 ．
（
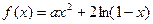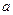为实数）.
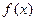在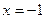
处有极值，求
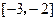上是增函数，求
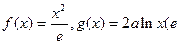为自然对数的底数，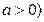
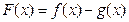的最小值；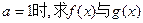
图象的一个公共点坐标，并求它们在该公共点处的切线方程。（14分）
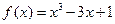在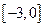
上的最大值与最小值的差为 .
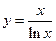在区间
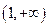上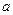
为实数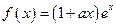，函数
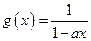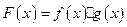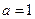，函数
，
．
，求函数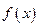
的极小值；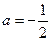
时，解不等式
；
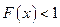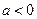时，求函数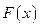
的单调区间．