题目内容
(本小题满分12分)
设f(x)是定义在[-1,1]上的奇函数,对于任意的
 当
当 时,都
时,都
有
(1)若函数g(x)=f(x-c)和h(x)=f(x-c2)的定义域的交集是空集,求c的取值范围;
(2)判断函数f(x)在[-1,1]上的单调性,并用定义证明。
(1){x|c<-1或c>2}
(2)增函数
解析

练习册系列答案
相关题目
已知二次函数 的导函数为
的导函数为 ,且
,且 >0,
>0, 的图象与x
的图象与x
轴恰有一个交点,则 的最小值为 ( )
的最小值为 ( )
| A.3 | B. | C.2 | D. |

 的定义域为R,当x<0时,
的定义域为R,当x<0时, .
. ,判断并证明函数
,判断并证明函数 满足
满足 ,且
,且 ,
, 时,不等式
时,不等式 对不小于2的正整数
对不小于2的正整数 对任意
对任意 ,都有
,都有 ,
, > 0时,
> 0时, < 0,
< 0, .
.  ;
;  时,
时,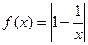 ,(x>0).
,(x>0).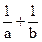 的值 ;
的值 ;  若存在实数a,b(a<b),使得函数y=f(x)的定义域为 [a,b]时,值域为 [
若存在实数a,b(a<b),使得函数y=f(x)的定义域为 [a,b]时,值域为 [ ma,mb],(m≠0),求m的取值范围.
ma,mb],(m≠0),求m的取值范围. 

 构成的面积为
构成的面积为
 的十字型地域,计划在正方形
的十字型地域,计划在正方形 上建一座“观景花坛”,
上建一座“观景花坛”, 元/
元/ 元/
元/ 等)上铺草坪,造价为
等)上铺草坪,造价为 元/
元/ 元,
元, 长为
长为
 ,试建立
,试建立 为偶函数,且其图像上相邻的一个最高点和最低点之间的距离为
为偶函数,且其图像上相邻的一个最高点和最低点之间的距离为 。
。 的值。
的值。 论函数
论函数 的奇偶性,并说明理由.
的奇偶性,并说明理由.