题目内容
【题目】已知椭圆C:![]() (a>b>0)的焦点F与抛物线E:y2=4x的焦点重合,直线x-y+
(a>b>0)的焦点F与抛物线E:y2=4x的焦点重合,直线x-y+![]() =0与以原点O为圆心,以椭圆的离心率e为半径的圆相切.
=0与以原点O为圆心,以椭圆的离心率e为半径的圆相切.
(Ⅰ)直线x=1与椭圆交于不同的两点M,N,椭圆C的左焦点F1,求△F1MN的内切圆的面积;
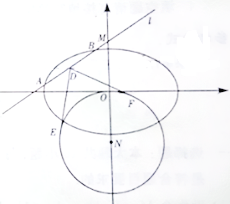
(Ⅱ)直线l与抛物线E交于不同两点A,B,直线l′与抛物线E交于不同两点C,D,直线l与直线l′交于点M,过焦点F分别作l与l′的平行线交抛物线E于P,Q,G,H四点.证明:![]()
【答案】(Ⅰ) ![]() ;(Ⅱ)见解析.
;(Ⅱ)见解析.
【解析】试题分析:(Ⅰ)利用条件得椭圆方程,将x=1代入椭圆得M,N坐标,求出△F1MN的周长和面积,进而得内切圆半径;
(Ⅱ)设出直线方程与椭圆联立,利用韦达定理结合弦长公式表示弦长,进而化简运算即可证明.
试题解析:
(Ⅰ) 依题意,得c=1,e=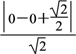 =
=![]() ,
,
即![]() =
=![]() ,∴a=2,∴b=
,∴a=2,∴b=![]() ,∴所求椭圆C的方程为
,∴所求椭圆C的方程为![]() +
+![]() =1.
=1.
直线l的方程为x=1,得M![]() ,N
,N![]() ,
,
设△F1MN的内切圆的半径为R,
则△F1MN的周长=4a=8,S△F1MN=![]() (|MN|+|F1M|+|F1N|)R=4R.
(|MN|+|F1M|+|F1N|)R=4R.
又因为S△F1MN=3=4R,∴R=![]() ,所求内切圆的面积为
,所求内切圆的面积为![]() π.
π.
(Ⅱ)设直线l和l′的方程分别为x=k1y+m1,x=k2y+m2,
设A(x1,y1),B(x2,y2),C(x3,y3),D(x4,y4),
由方程组![]() 得
得
y2-4k1y-4m1=0 ①
方程①的判别式Δ>0,得4k12+4m1>0.
由①得y1+y2=4k1,y1y2=-4m1,
由方程组![]() 得
得
y2-4k2y-4m2=0 ②
方程②的判别式Δ>0,得4k22+4m2>0.
由②得y3+y4=4k2,y3y4=-4m2.
联立直线l与直线l′的方程可得:M点坐标为![]() .
.
因为|MA|·|MB|=(1+k12)![]() ,代入计算得,
,代入计算得,
|MA|·|MB|=![]() ·|(m2-m1)2+4k1k2(m1+m2)-4(m1k22+m2k12)|.
·|(m2-m1)2+4k1k2(m1+m2)-4(m1k22+m2k12)|.
同理可得
|MC|·|MD|=(1+k22)![]() =
=
![]() ·
·![]() .
.
因此![]() =
=![]() .
.
由于PQ,HG分别与直线l和直线l′平行,故可设其方程分别为x=k1y+1,x=k2y+1.
由方程组![]() 得
得
y2-4k1y-4=0. ③
由③得yP+yQ=4k1,yPyQ=-4,
因此|PQ|=xP+xQ+p=k1(yP+yQ)+4=4(1+k12).
同理可得|HG|=xH+xG+p=k1(yH+yG)+4=4(1+k22).
故![]() =
=![]() .
.
所以![]() =
=![]() .
.