Question

【题目】对于定义域为D的函数y=f（x），若同时满足下列条件：
①f（x）在D内单调递增或单调递减；
②存在区间[a，b]D，使f（x）在[a，b]上的值域为[a，b]，则把y=f（x），x∈D叫闭函数．
（1）求闭函数y=x3符合条件②的区间[a，b]；
（2）判断函数f（x）= x+ ，（x＞0）是否为闭函数？并说明理由；
（3）已知[a，b]是正整数，且定义在（1，m）的函数y=k﹣ 是闭函数，求正整数m的最小值，及此时实数k的取值范围．

Answer 1

【答案】
（1）解：由题意，y=x3在[a，b]上递增，在[a，b]上的值域为[a，b]，

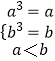∴ ，求得 ．

所以，所求的区间[a，b]为[﹣1，1]

（2）解：取 x1=1，x2=10，则f（x1）= ＜ =f（x2），

即f（x）不是（0，+∞）上的减函数．

取 x1= ，x2= ，则f（x1）= +10＜ +100=f（x2），

即f（x）不是（0，+∞）上的增函数，

所以，函数在定义域内不单调递增或单调递减，从而该函数不是闭函数

（3）解：函数y=k﹣ 是闭函数，则存在区间[a，b]，使函数f（x）的值域为[a，b]，

∵函数y=k﹣ 在区间[a，b]上单调递增，即 ，

∴a，b为方程 的两个实根，

即方程 在（1，m）上有两个不等的实根．

由于 ，

考察函数 ，∵函数g（x）在（1，2）上递减，∴m＞2．

∵g（x）在（2，m）递增，而函数y=g（x）与y=k在（1，m）有两个交点， ，

∵ ，

所以正整数m的最小值为3，此时，g（3）= ，此时，k的范围是（5， ）．

【解析】（1）由题意，y=x3在[a，b]上递增，在[a，b]上的值域为[a，b]，故有 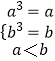，求得a、b的值，可得结论．（2）取 x1=1，x2=10，则由f（x1）= ＜ =f（x2），可得f（x）不是（0，+∞）上的减函数．同理求得f（x）不是（0，+∞）上的增函数，从而该函数不是闭函数．（3）由题意，可得方程 在（1，m）上有两个不等的实根．利用基本不等式求得当x=2时，k取得最小值为5．再根据函数g（x）在（1，2）上递减，在（2，m）递增，而函数y=g（x）与y=k在（1，m）有两个交点，可得正整数m的最小值为3，此时，g（3）= ，由此求得k的范围．
【考点精析】认真审题，首先需要了解函数的定义域及其求法(求函数的定义域时，一般遵循以下原则：①是整式时，定义域是全体实数;②是分式函数时，定义域是使分母不为零的一切实数;③是偶次根式时，定义域是使被开方式为非负值时的实数的集合;④对数函数的真数大于零，当对数或指数函数的底数中含变量时，底数须大于零且不等于1,零（负）指数幂的底数不能为零)，还要掌握函数单调性的性质(函数的单调区间只能是其定义域的子区间 ,不能把单调性相同的区间和在一起写成其并集)的相关知识才是答题的关键．