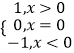Question

【题目】在平面直角坐标系xOy中,已知椭圆C: (a>b>0)的离心率为,椭圆C截直线y=1所得线段的长度为.

(Ⅰ)求椭圆C的方程；

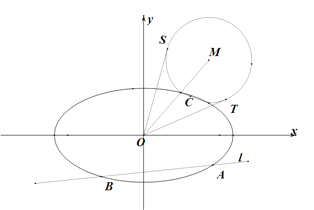
(Ⅱ)动直线l:y=kx+m(m≠0)交椭圆C于A,B两点,交y轴于点M.点N是M关于O的对称点,⊙N的半径为|NO|. 设D为AB的中点,DE,DF与⊙N分别相切于点E,F,求EDF的最小值.

Answer 1

【答案】（Ⅰ） .(II) .

【解析】试题分析：（Ⅰ）由得,由椭圆C截直线y=1所得线段的长度为,得,求得椭圆的方程为；（Ⅱ）由,解得,确定,,

结合的单调性求的最小值.

试题解析：（Ⅰ）由椭圆的离心率为，得，

又当时， ，得，

所以，

因此椭圆方程为.

（Ⅱ）设，

联立方程，

得，

由得.（*）

且，

因此，

所以，

又，

所以

整理得 ，

因为，

所以.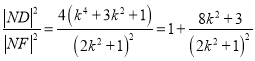

令，

故，

所以 .

令，所以.

当时， ,

从而在上单调递增，

因此，

等号当且仅当时成立，此时，

所以，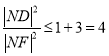

由（*）得 且.

故，

设，

则 ，

所以的最小值为，

从而的最小值为，此时直线的斜率是.

综上所述：当， 时， 取到最小值.