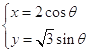题目内容
【题目】已知曲线 ![]() 的参数方程为
的参数方程为 ![]() (
( ![]() 为参数),在同一平面直角坐标系中,将曲线
为参数),在同一平面直角坐标系中,将曲线 ![]() 上的点按坐标变换
上的点按坐标变换  得到曲线
得到曲线 ![]() .
.
(1)求曲线 ![]() 的普通方程;
的普通方程;
(2)若点 ![]() 在曲线
在曲线 ![]() 上,点
上,点 ![]()
![]() ,当点
,当点 ![]() 在曲线
在曲线 ![]() 上运动时,求
上运动时,求 ![]() 中点
中点 ![]() 的轨迹方程.
的轨迹方程.
【答案】
(1)解: : ![]() ,
,
将 代入 的普通方程得 ,即 ![]() ;
;
(2)解:设 , 则
所以 ,即
代入 ![]() ,得 ,即
,得 ,即
中点 的轨迹方程为 .
【解析】分析:本题主要考查了椭圆的参数方程;圆的参数方程,解决问题的关键是(1)将参数方程转化为直角坐标系下的普通方程,需要根据参数方程的结构特征,选取恰当的消参方法,常见的消参方法有:代入消参法、加减消参法、平方消参法;(2)将参数方程转化为普通方程时,要注意两种方程的等价性,不要增解、漏解,若 ![]() 有范围限制,要标出
有范围限制,要标出 ![]() 的取值范围;(3)直角坐标方程化为极坐标方程,只需把公式
的取值范围;(3)直角坐标方程化为极坐标方程,只需把公式 ![]() 及
及 ![]() 直接代入并化简即可;而极坐标方程化为极坐标方程要通过变形,构造形如
直接代入并化简即可;而极坐标方程化为极坐标方程要通过变形,构造形如 ![]() ,
, ![]() ,
, ![]() 的形式,进行整体代换,其中方程的两边同乘以(或同除以)
的形式,进行整体代换,其中方程的两边同乘以(或同除以) ![]() 及方程的两边平方是常用的变形方法.
及方程的两边平方是常用的变形方法.
【考点精析】本题主要考查了圆的参数方程和椭圆的参数方程的相关知识点,需要掌握圆![]() 的参数方程可表示为
的参数方程可表示为![]() ;椭圆
;椭圆![]()
![]() 的参数方程可表示为
的参数方程可表示为![]() 才能正确解答此题.
才能正确解答此题.

练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目