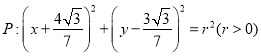题目内容

【题目】已知圆的一条直角是椭圆的长轴，动直线，当过椭圆上一点且与圆相交于点时，弦的最小值为.

（1）求圆即椭圆的方程；

（2）若直线是椭圆的一条切线，是切线上两个点，其横坐标分别为，那么以为直径的圆是否经过轴上的定点？如果存在，求出定点坐标；若不存在，请说明理由.

【答案】（1）.（2）过定点与.

【解析】试题分析:（1）先根据垂径定理求半径，再根据点在椭圆上解得，（2）设点的坐标，化简条件，再联立切线方程与椭圆方程，根据判别式为零得等量关系，代入并化简可得，即得结论

试题解析：（1）当时，最小，，

由已知，可知，

又点在椭圆上上，

综上，圆的方程为，

椭圆的方程为.

（2）联立方程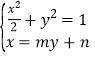，得到，由与椭圆相切，得到，①

易知，设以为直径的圆经过，设则有，

而，②

由①②可知， ，

要使上式成立，有只有当，故经过定点与.

练习册系列答案
相关题目

【题目】如图， 是边长为3的正方形， 平面， 平面， .

（1）证明：平面平面；

（2）在上是否存在一点，使平面将几何体分成上下两部分的体积比为？若存在，求出点的位置；若不存在，请说明理由.

【题目】下列关于古典概型的说法中正确的是( )

①试验中所有可能出现的基本事件只有有限个；

②每个事件出现的可能性相等；

③每个基本事件出现的可能性相等；

④基本事件的总数为n，随机事件A若包含k个基本事件，则.

A. ②④ B. ③④ C. ①④ D. ①③④

【题目】某公司为确定下一年度投入某种产品的宣传费，需了解年宣传费x(单位：千元)对年销售量y(单位：t)和年利润z(单位：千元)的影响．对近8年的年宣传费xi和年销售量yi(i＝1,2，…，8)数据作了初步处理，得到下面的散点图及一些统计量的值．

表中 ，

（Ⅰ）根据散点图判断，y=a+bx与y=c+d哪一个适宜作为年销售量y关于年宣传费x的回归方程类型？（给出判断即可，不必说明理由）

（Ⅱ）根据（Ⅰ）的判断结果及表中数据，建立y关于x的回归方程；

（Ⅲ）已知这种产品的年利润z与x、y的关系为z=0.2y-x.根据（Ⅱ）的结果回答下列问题：

(ⅰ)年宣传费x=49时，年销售量及年利润的预报值是多少？

(ⅱ)年宣传费x为何值时，年利润的预报值最大？

附：对于一组数据,，……，,其回归线的斜率和截距的最小二乘估计分别为：

46.6

563

6.8

289.8

1.6

1469

108.8

，

【题目】设点为椭圆的左焦点，直线被椭圆截得弦长为．

（1）求椭圆的方程；

（2）圆与椭圆交于两点， 为线段上任意一点，直线交椭圆于两点为圆的直径，且直线的斜率大于，求的取值范围．

【题目】已知函数.

(1)若对恒成立，求实数的取值范围；

(2)已知关于的方程有两个实根，求证： .

【题目】某篮球队甲、乙两名运动员练习罚球，每人练习10组，每组罚球40个．命中个数的茎叶图如图，则下面结论中错误的一个是(　　)

A. 甲的极差是29 B. 甲的中位数是24

C. 甲罚球命中率比乙高 D. 乙的众数是21

【题目】某学校因为寒假延期开学，根据教育部停课不停学的指示，该学校组织学生线上教学，高一年级在线上教学一个月后，为了了解线上教学的效果，在线上组织了数学学科考试，随机抽取50名学生的成绩并制成频率分布直方图如图所示.

（1）求m的值，并估计高一年级所有学生数学成绩在分的学生所占的百分比；

（2）分别估计这50名学生数学成绩的平均数和中位数.（同一组中的数据以该组区间的中点值作代表，结果精确到0.1）

【题目】某种产品的广告费支出与销售额 (单位：万元）具有较强的相关性，且两者之间有如下对应数据:

2

4

5

6

8

28

36

52

56

78

（1）求关于的线性回归方程；

（2）根据（1）中的线性回归方程，当广告费支出为10万元时，预测销售额是多少？

参考数据： ，，。

附：回归方程中斜率和截距的最小二乘估计公式分别为：

，.

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网