题目内容
如图,已知△P1OP2的面积为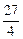 ,P为线段P1P2的一个三等分点,求以直线OP1、OP2为渐近线且过点P的离心率为
,P为线段P1P2的一个三等分点,求以直线OP1、OP2为渐近线且过点P的离心率为 的双曲线方程.
的双曲线方程. 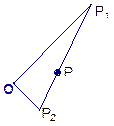
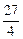 ,P为线段P1P2的一个三等分点,求以直线OP1、OP2为渐近线且过点P的离心率为
,P为线段P1P2的一个三等分点,求以直线OP1、OP2为渐近线且过点P的离心率为 的双曲线方程.
的双曲线方程. 
双曲线方程为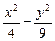 =1
=1
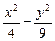 =1
=1 以O为原点,∠P1OP2的角平分线为x轴建立如图的直角坐标系.
设双曲线方程为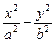 =1(a>0,b>0)
=1(a>0,b>0)
由e2=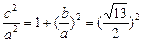 ,得
,得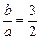 .
.
∴两渐近线OP1、OP2方程分别为y=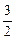 x和y=-
x和y=-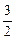 x
x
设点P1(x1,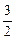 x1),P2(x2,-
x1),P2(x2,-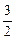 x2)(x1>0,x2>0),则由点P分
x2)(x1>0,x2>0),则由点P分 所成的比λ=
所成的比λ= =2,得P点坐标为(
=2,得P点坐标为(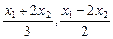 ),又点P在双曲线
),又点P在双曲线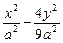 =1上,所以
=1上,所以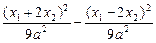 =1,
=1,
即(x1+2x2)2-(x1-2x2)2=9a2,整理得8x1x2=9a2 ①
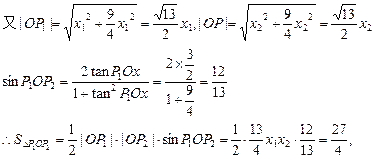
即x1x2=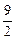 ②
②
由①、②得a2=4,b2=9
故双曲线方程为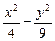 =1.
=1.
设双曲线方程为
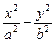 =1(a>0,b>0)
=1(a>0,b>0)由e2=
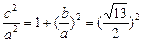 ,得
,得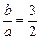 .
.∴两渐近线OP1、OP2方程分别为y=
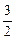 x和y=-
x和y=-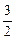 x
x设点P1(x1,
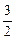 x1),P2(x2,-
x1),P2(x2,-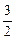 x2)(x1>0,x2>0),则由点P分
x2)(x1>0,x2>0),则由点P分 所成的比λ=
所成的比λ= =2,得P点坐标为(
=2,得P点坐标为(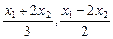 ),又点P在双曲线
),又点P在双曲线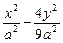 =1上,所以
=1上,所以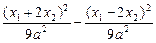 =1,
=1,即(x1+2x2)2-(x1-2x2)2=9a2,整理得8x1x2=9a2 ①
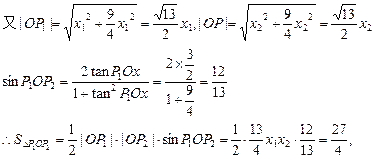
即x1x2=
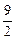 ②
②由①、②得a2=4,b2=9
故双曲线方程为
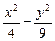 =1.
=1.
练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
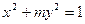 的渐近线过点(-1,2),则该双曲线的虚轴的长是______________。
的渐近线过点(-1,2),则该双曲线的虚轴的长是______________。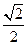 围成的三角形区域(包含边界)为E,P(x,y)为该区域内的一个动点,则目标函数
围成的三角形区域(包含边界)为E,P(x,y)为该区域内的一个动点,则目标函数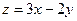 的取值范围为 ( )
的取值范围为 ( ) 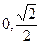 ]
]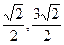 ]
]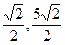 ]
]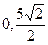 ]
] 到其渐近线的距离为
到其渐近线的距离为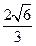 .若过
.若过 点作斜率为
点作斜率为 的直线交双曲线于
的直线交双曲线于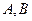 两点,交
两点,交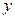 轴于
轴于 点,且
点,且 是
是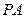 与
与 的等比中项,则双曲线的半焦距为__________.
的等比中项,则双曲线的半焦距为__________. 的离心率e=2,A,B为双曲线上两点,线段AB的垂直平分线为
的离心率e=2,A,B为双曲线上两点,线段AB的垂直平分线为
 的最小值为3,若存在求出所有可能的a值,若不存在说明理由.
的最小值为3,若存在求出所有可能的a值,若不存在说明理由.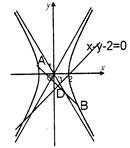
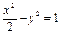 有相同的渐近线的双曲线方程是 ( )
有相同的渐近线的双曲线方程是 ( )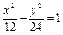
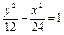
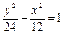
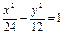

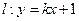 与双曲线
与双曲线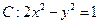 的右支交于不同两点
的右支交于不同两点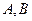 ,(1)求实数
,(1)求实数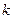 的取值范围;(2)是否存在实数
的取值范围;(2)是否存在实数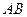 为直径的圆经过双曲线右焦点
为直径的圆经过双曲线右焦点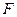 ?若存在,求出
?若存在,求出