题目内容
直线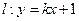 与双曲线
与双曲线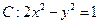 的右支交于不同两点
的右支交于不同两点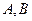 ,(1)求实数
,(1)求实数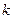 的取值范围;(2)是否存在实数
的取值范围;(2)是否存在实数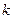 ,使得以线段
,使得以线段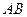 为直径的圆经过双曲线右焦点
为直径的圆经过双曲线右焦点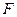 ?若存在,求出
?若存在,求出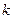 的值,若不存在,请说明理由。
的值,若不存在,请说明理由。
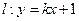 与双曲线
与双曲线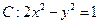 的右支交于不同两点
的右支交于不同两点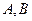 ,(1)求实数
,(1)求实数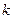 的取值范围;(2)是否存在实数
的取值范围;(2)是否存在实数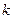 ,使得以线段
,使得以线段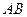 为直径的圆经过双曲线右焦点
为直径的圆经过双曲线右焦点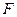 ?若存在,求出
?若存在,求出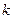 的值,若不存在,请说明理由。
的值,若不存在,请说明理由。⑴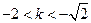 ⑵
⑵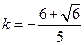 可使得以线段AB为直径的圆过双曲线的右焦点。
可使得以线段AB为直径的圆过双曲线的右焦点。
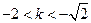 ⑵
⑵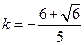 可使得以线段AB为直径的圆过双曲线的右焦点。
可使得以线段AB为直径的圆过双曲线的右焦点。(1)将直线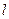 的方程代入双曲线
的方程代入双曲线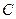 的方程
的方程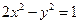 后,整理得:
后,整理得: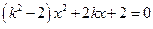 ---①,依题意,直线与双曲线
---①,依题意,直线与双曲线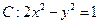 的右支交于不同两点
的右支交于不同两点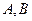 ,∴
,∴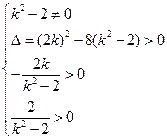 ,解得
,解得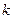 的取值范围是
的取值范围是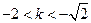 。
。
(2)设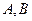 两点的坐标分别是
两点的坐标分别是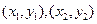 ,则由①式得
,则由①式得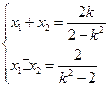 ----②,假设存在实数
----②,假设存在实数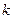 使得以线段
使得以线段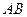 为直径的圆经过双曲线右焦点
为直径的圆经过双曲线右焦点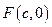 ,则由
,则由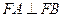 得
得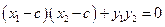 ,即
,即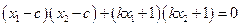 ------③,整理得:
------③,整理得: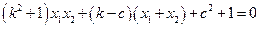 ,把②式及
,把②式及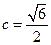 代入③式化简得
代入③式化简得 ,解得
,解得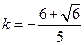 或
或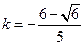 ,又
,又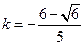 不符合
不符合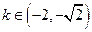 ,所以舍去。可知
,所以舍去。可知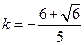 可使得以线段AB为直径的圆过双曲线的右焦点。
可使得以线段AB为直径的圆过双曲线的右焦点。
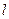 的方程代入双曲线
的方程代入双曲线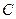 的方程
的方程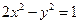 后,整理得:
后,整理得: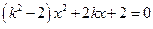 ---①,依题意,直线与双曲线
---①,依题意,直线与双曲线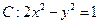 的右支交于不同两点
的右支交于不同两点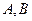 ,∴
,∴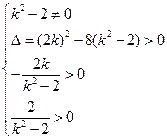 ,解得
,解得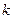 的取值范围是
的取值范围是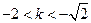 。
。(2)设
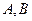 两点的坐标分别是
两点的坐标分别是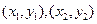 ,则由①式得
,则由①式得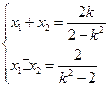 ----②,假设存在实数
----②,假设存在实数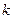 使得以线段
使得以线段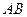 为直径的圆经过双曲线右焦点
为直径的圆经过双曲线右焦点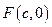 ,则由
,则由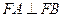 得
得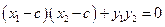 ,即
,即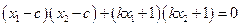 ------③,整理得:
------③,整理得: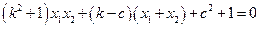 ,把②式及
,把②式及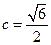 代入③式化简得
代入③式化简得 ,解得
,解得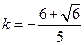 或
或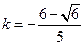 ,又
,又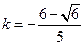 不符合
不符合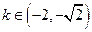 ,所以舍去。可知
,所以舍去。可知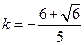 可使得以线段AB为直径的圆过双曲线的右焦点。
可使得以线段AB为直径的圆过双曲线的右焦点。
练习册系列答案
 激活思维优加课堂系列答案
激活思维优加课堂系列答案 活力试卷系列答案
活力试卷系列答案
相关题目
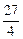 ,P为线段P1P2的一个三等分点,求以直线OP1、OP2为渐近线且过点P的离心率为
,P为线段P1P2的一个三等分点,求以直线OP1、OP2为渐近线且过点P的离心率为 的双曲线方程.
的双曲线方程. 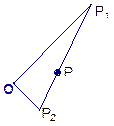
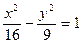
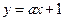 与双曲线
与双曲线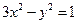 交于
交于 两点,(1)求
两点,(1)求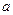 的取值范围;(2)若以
的取值范围;(2)若以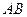 为直径的圆过坐标原点,求实数
为直径的圆过坐标原点,求实数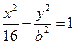
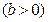 的一条准线恰好是圆
的一条准线恰好是圆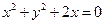 的一条切线,则
的一条切线,则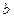 等于( )
等于( )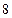
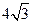
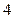
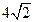
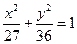 有共同的焦点,且与椭圆的一个交点的纵坐标为
有共同的焦点,且与椭圆的一个交点的纵坐标为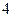 ,求双曲线的方程。
,求双曲线的方程。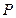 到点
到点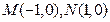 的距离之差为
的距离之差为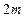 ,到
,到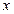 轴的距离与到
轴的距离与到 轴的距离之比为
轴的距离之比为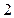 ,求
,求 的取值范围。
的取值范围。 是双曲线
是双曲线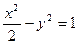 的左、右焦点,P、Q为右支上的两点,直线PQ过
的左、右焦点,P、Q为右支上的两点,直线PQ过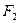 ,且倾斜角为
,且倾斜角为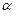 ,则
,则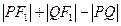 的值为 ( )
的值为 ( )
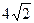 B
B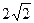 D
D 的离心率
的离心率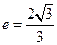 ,则实数
,则实数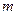 的值是 。
的值是 。