题目内容
【题目】已知椭圆C的中心在原点O，焦点在x轴上，离心率为 
，椭圆C上的点到右焦点的最大距离为3．
（1）求椭圆C的标准方程；
（2）斜率存在的直线l与椭圆C交于A，B两点，并且满足|2 
+ 
|=|2 ﹣ |，求直线在y轴上截距的取值范围．
【答案】
（1）解：设椭圆C的方程为： 
=1（a＞b＞0），半焦距为c．
依题意e= 
= 
，由椭圆C上的点到右焦点的最大距离3，得a+c=3，解得c=1，a=2，
∴b2=a2﹣c2=3，
∴椭圆C的标准方程是 
=1
（2）解：设直线l的方程为y=kx+m，联立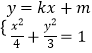 
，化为：（3+4k2）x2+8kmx+4m2﹣12=0，
△=64k2m2﹣4（3+4k2）（4m2﹣12）＞0，化简得3+4k2＞m2．
设A（x1，y1），B（x2，y2），
则x1+x2=﹣ 
，x1x2= 
，
∵|2 
+ 
|=|2 ﹣ |，∴ 
=0．
∴x1x2+y1y2=0，即x1x2+（kx1+m）（kx2+m）=0，化为km（x1+x2）+（1+k2）x1x2+m2=0，
∴km（﹣ ）+（1+k2）× +m2=0，
化简得7m2=12+12k2．
将k2= 
﹣1代入3+4k2＞m2．
可得m2 
，又由7m2=12+12k2≥12．
从而∴m2 
，解得m≥ 
，或m≤﹣ ，．
所以实数m的取值范围是 
∪ 
【解析】（1）设椭圆C的方程为： =1（a＞b＞0），半焦距为c．依题意e= = ，a+c=3，b2=a2﹣c2 ， 解出即可得出．（2）设直线l的方程为y=kx+m，与椭圆方程联立化为：（3+4k2）x2+8kmx+4m2﹣12=0，△＞0，设A（x1 ， y1），B（x2 ， y2）．由|2 + |=|2 ﹣ |，可得 =0．x1x2+y1y2=0，即x1x2+（kx1+m）（kx2+m）=0，把根与系数的关系代入化简与△＞0联立解出即可得出．
