题目内容
【题目】已知点![]() ,
,![]() ,
,![]() 在抛物线
在抛物线![]() 上,
上,![]() 的重心与此抛物线的焦点
的重心与此抛物线的焦点![]() 重合(如图)
重合(如图)

(I)写出该抛物线的方程和焦点![]() 的坐标;
的坐标;
(II)求线段![]() 中点
中点![]() 的坐标;
的坐标;
(III)求弦![]() 所在直线的方程
所在直线的方程
【答案】(1)抛物线方程为![]() ,焦点F的坐标为(8,0)。.
,焦点F的坐标为(8,0)。.
(2)M的坐标为(11,-4)。
(3)BC所在直线的方程为:![]()
【解析】
解:(1)由点A(2,8)在抛物线![]() 上,有
上,有![]() ,
,
解得p="16." 所以抛物线方程为![]() ,焦点F的坐标为(8,0)
,焦点F的坐标为(8,0)
(2)由于F(8,0)是△ABC的重心,M是BC的中点,所以F分AM的比为2:1,即![]() ,设点M的坐标为
,设点M的坐标为![]() ,则
,则![]()
解得![]() , 所以点M的坐标为(11,-4)
, 所以点M的坐标为(11,-4)
(3)由于线段BC的中点M不在x轴上,所以BC所在
的直线不垂直于x轴.设BC所在直线的方程为:![]()
由![]() 消x得
消x得![]() ,
,
所以![]() ,由(2)的结论得
,由(2)的结论得![]() ,解得
,解得![]()
因此BC所在直线的方程为:![]()

练习册系列答案
相关题目
【题目】如今,中国的“双十一”已经从一个节日变成了全民狂欢的“电商购物日”.某淘宝电商分析近8年“双十一”期间的宣传费用![]() (单位:万元)和利润
(单位:万元)和利润![]() (单位:十万元)之间的关系,得到下列数据:
(单位:十万元)之间的关系,得到下列数据:
| 2 | 3 | 4 | 5 | 6 | 8 | 9 | 11 |
| 1 | 2 | 3 | 3 | 4 | 5 | 6 | 8 |
请回答:
(Ⅰ)请用相关系数![]() 说明
说明![]() 与
与![]() 之间是否存在线性相关关系(当
之间是否存在线性相关关系(当![]() 时,说明
时,说明![]() 与
与![]() 之间具有线性相关关系);
之间具有线性相关关系);
(Ⅱ)根据1的判断结果,建立![]() 与
与![]() 之间的回归方程,并预测当
之间的回归方程,并预测当![]() 时,对应的利润
时,对应的利润![]() 为多少(
为多少(![]() 精确到
精确到![]() ).
).
附参考公式:回归方程中![]() 中
中![]() 和
和![]() 最小二乘估计分别为
最小二乘估计分别为 ,
,![]() ,
,
相关系数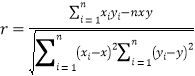 .
.
参考数据: ![]() .
.