题目内容
【题目】在
中，角
，
，
的对边分别为
，
，
，
，且
，则面积的最大值为（ ）
A. 
B. 
C. 
D. 
【答案】B
【解析】
利用余弦定理分别表示出cosB和cosA，代入到已知的等式中，化简后即可求出c的值，然后利用余弦定理表示出c2=a2+b2﹣2abcosC，把c及cosC的值代入后，利用基本不等式即可求出ab的最大值，然后由cosC的值，及C的范围，利用同角三角函数间的基本关系求出sinC的值，利用三角形的面积公式表示出三角形ABC的面积，把ab的最大值及sinC的值代入即可求出面积的最大值．
∵acosB+bcosA=2，
∴
∴c=2，
∴4=a2+b2﹣2ab×
≥2ab﹣2ab×=
ab，
∴ab≤
（当且仅当a=b=
时等号成立）
由cosC=，得sinC=
，
∴S△ABC=
absinC≤××=
，
故△ABC的面积最大值为．
故答案为：
．
练习册系列答案
阅读快车系列答案
相关题目
【题目】如今,中国的“双十一”已经从一个节日变成了全民狂欢的“电商购物日”.某淘宝电商分析近8年“双十一”期间的宣传费用
(单位:万元)和利润
(单位:十万元)之间的关系,得到下列数据:
| 2 | 3 | 4 | 5 | 6 | 8 | 9 | 11 |
| 1 | 2 | 3 | 3 | 4 | 5 | 6 | 8 |
请回答:
（Ⅰ）请用相关系数
说明与之间是否存在线性相关关系(当
时,说明与之间具有线性相关关系);
（Ⅱ）根据1的判断结果,建立与之间的回归方程,并预测当
时,对应的利润
为多少(
精确到
).
附参考公式:回归方程中
中
和
最小二乘估计分别为
,
,
相关系数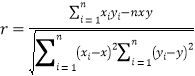
.
参考数据: 
.
