题目内容
16.函数y=f(x)与y=g(x)的图象如图,则函数y=f(x)•g(x)的图象为( )
| A. |  | B. | 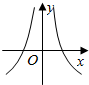 | C. | 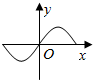 | D. | 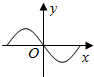 |
分析 由图象得到函数f(x)和g(x)的奇偶性和函数的定义域,继而得到=f(x)•g(x)为奇函数,且定义域为{x|x≠0},问题得以解决.
解答 解:由图象可知,y=f(x)为偶函数,其定义域为R,y=g(x)为奇函数,其定义域为{x|x≠0}
∴f(-x)•g(x)=-f(x)•g(x),
∴y=f(x)•g(x)为奇函数,且定义域为{x|x≠0}
∴f(x)•g(x)的图象关于原点对称,
故选:A.
点评 本题考查了函数的奇偶性和函数图象的识别,属于基础题.

练习册系列答案
 名题金卷系列答案
名题金卷系列答案 优加精卷系列答案
优加精卷系列答案
相关题目
6.已知集合A={y|y=log2x,x>1},B={y|y=($\frac{1}{2}$)x,x>2},则A∩B等于( )
| A. | {y|0$<y<\frac{1}{4}$} | B. | {y|0<y<1} | C. | {y|$\frac{1}{4}$<y<1} | D. | ∅ |
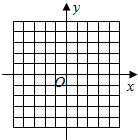 设f(x)=x2-2|x|-3,在下列直角坐标系中画出f(x)的图象.
设f(x)=x2-2|x|-3,在下列直角坐标系中画出f(x)的图象.