题目内容
已知数列 满足:
满足: ,
, ,
, ,那么使
,那么使 成立的
成立的 的最大值为( )
的最大值为( )
| A.4 | B.5 | C.24 | D.25 |
C
解析试题分析: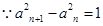 ,
,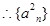 是以
是以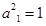 ,公差为1 的等差数列,则
,公差为1 的等差数列,则 ,又
,又 ,
,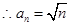 ,故
,故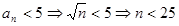 ,故使
,故使 成立的
成立的 的最大值为24
的最大值为24
考点:等差数列,等比数列

练习册系列答案
相关题目
若数列{an}是等比数列,且an>0,则数列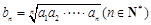 也是等比数列. 若数列
也是等比数列. 若数列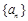 是等差数列,可类比得到关于等差数列的一个性质为( ).
是等差数列,可类比得到关于等差数列的一个性质为( ).
A.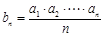 是等差数列 是等差数列 |
B.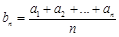 是等差数列 是等差数列 |
C.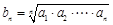 是等差数列 是等差数列 |
D.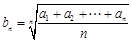 是等差数列 是等差数列 |
如图,一条螺旋线是用以下方法画成: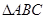 是边长为1的正三角形,曲线
是边长为1的正三角形,曲线 是分别以
是分别以 为圆心,
为圆心, 为半径画的弧,曲线
为半径画的弧,曲线 记为螺旋线旋第一圈.然后又以
记为螺旋线旋第一圈.然后又以 为圆心
为圆心 为半径画弧,
为半径画弧,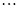
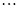 这样画到第
这样画到第 圈,则所得螺旋线的长度
圈,则所得螺旋线的长度 为( )
为( )
A. | B. | C. | D. |
已知等差数列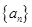 的前
的前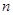 项和为
项和为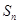 ,且
,且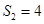 ,
,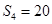 ,则该数列的公差
,则该数列的公差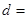 ( )
( )
A. | B.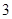 | C.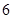 | D.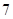 |
等差数列 的前n项和为
的前n项和为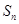 ,已知
,已知 ,
,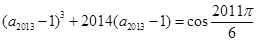 ,则
,则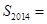 ( )
( )
| A.2014 | B.4028 | C.0 | D.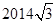 [ [ |
若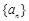 是等差数列,首项
是等差数列,首项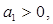
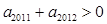 ,
,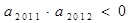 ,则使前n项和
,则使前n项和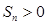 成立的最大正整数n是( )
成立的最大正整数n是( )
| A.2011 | B.2012 | C.4022 | D.4023 |
在等差数列{an}中,a1=-28,公差d=4,若前n项和Sn取得最小值,则n的值为( )
| A.7 | B.8 | C.7或8 | D.8或9 |
在各项均不为零的等差数列{an}中,若 -an+1=an-1(n≥2,n∈N*),则S2014的值为( )
-an+1=an-1(n≥2,n∈N*),则S2014的值为( )
| A.2013 | B.2014 | C.4026 | D.4028 |
[2014·扬州质检]在等差数列{an}中,a1=-2014,其前n项和为Sn,若 -
- =2,则S2014的值等于 ( )
=2,则S2014的值等于 ( )
| A.-2011 | B.-2012 | C.-2013 | D.-2014 |