题目内容
若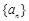 是等差数列,首项
是等差数列,首项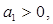
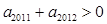 ,
,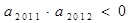 ,则使前n项和
,则使前n项和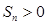 成立的最大正整数n是( )
成立的最大正整数n是( )
| A.2011 | B.2012 | C.4022 | D.4023 |
C
解析试题分析:∵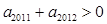 ,
,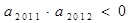 ,∴
,∴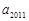 和
和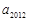 异号,且
异号,且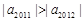 ,而
,而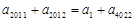 ,∵
,∵ ,∴
,∴ ,而
,而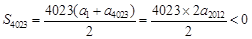 ,所以选C.
,所以选C.
考点:等差数列的性质、等差数列的前n项和公式.

练习册系列答案
相关题目
已知数列 满足:
满足: ,
, ,
, ,那么使
,那么使 成立的
成立的 的最大值为( )
的最大值为( )
| A.4 | B.5 | C.24 | D.25 |
首项为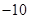 的等差数列,从第
的等差数列,从第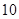 项起开始为正数,则公差
项起开始为正数,则公差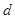 的取值范围是( ).
的取值范围是( ).
A. | B.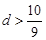 | C.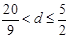 | D.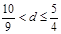 |
等差数列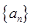 中,
中,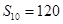 ,那么
,那么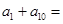 ( )
( )
A.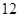 | B.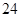 | C.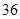 | D. |
数列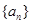 满足
满足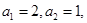 并且
并且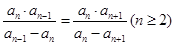 ,则数列
,则数列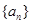 的第100项为( )
的第100项为( )
A.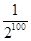 | B.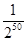 | C.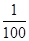 | D.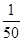 |
等差数列{an}的公差d<0,且a2·a4=12,a2+a4=8,则数列{an}的通项公式是( ).
| A.an=2n-2(n∈N*) | B.an=2n+4(n∈N*) |
| C.an=-2n+12(n∈N*) | D.an=-2n+10(n∈N*) |
设等差数列 的前
的前 项和为
项和为 ,若
,若 ,则
,则 等于( )
等于( )
A. | B. | C. | D. |
设数列{an}是等差数列,若a3+a4+a5=12,则a1+a2+…+a7=( )
| A.14 | B.21 | C.28 | D.35 |
在△ABC中,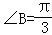 ,三边长a,b,c成等差数列,且ac=6,则b的值是( )
,三边长a,b,c成等差数列,且ac=6,则b的值是( )
A.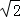 | B.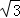 | C.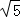 | D.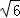 |