题目内容
等差数列 的前n项和为
的前n项和为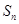 ,已知
,已知 ,
,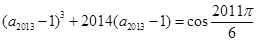 ,则
,则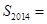 ( )
( )
| A.2014 | B.4028 | C.0 | D.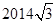 [ [ |
A
解析试题分析: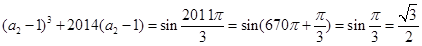
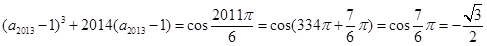 ,两式相加得
,两式相加得 ,解得
,解得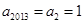 ,即数列
,即数列 为常数列,故
为常数列,故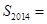 2014
2014
考点:等差数列的通项

练习册系列答案
相关题目
等差数列{an}的公差d < 0,且a2a4 = 12,a2 + a4 = 8,则数列{an}的通项公式是( )
| A.an = 2n-2 (n∈N*) | B.an =" 2n" + 4 (n∈N*) |
| C.an =-2n + 12 (n∈N*) | D.an =-2n + 10 (n∈N*) |
已知数列 满足:
满足: ,
, ,
, ,那么使
,那么使 成立的
成立的 的最大值为( )
的最大值为( )
| A.4 | B.5 | C.24 | D.25 |
已知等差数列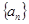 的前
的前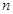 项和是
项和是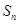 ,若
,若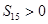 ,
,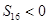 ,则
,则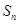 最大值是( )
最大值是( )
A.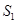 | B.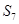 | C.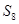 | D.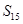 |
已知数列{an}中,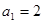 ,
,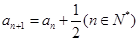 ,则
,则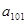 的值为 ( )
的值为 ( )
| A.49 | B.50 | C.51 | D.52 |
设等差数列 的前
的前 项和为
项和为 ,若
,若 ,则
,则 的值是( )
的值是( )
A. | B. | C. | D. |
首项为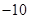 的等差数列,从第
的等差数列,从第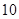 项起开始为正数,则公差
项起开始为正数,则公差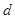 的取值范围是( ).
的取值范围是( ).
A. | B.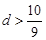 | C.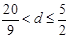 | D.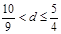 |
数列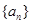 满足
满足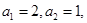 并且
并且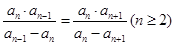 ,则数列
,则数列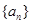 的第100项为( )
的第100项为( )
A.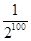 | B.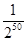 | C.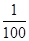 | D.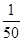 |
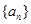 的前
的前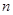 项和
项和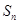 ,若
,若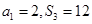 ,则
,则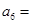 ( )
( )