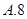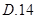题目内容
在等差数列{an}中,a1=-28,公差d=4,若前n项和Sn取得最小值,则n的值为( )
| A.7 | B.8 | C.7或8 | D.8或9 |
C
解析

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
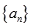 为等差数列,
为等差数列,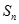 为前
为前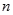 项和,
项和,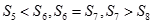 ,则下列错误的是( ).
,则下列错误的是( ).
A. | B. |
C. | D. 和 和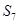 均为 均为 的最大值 的最大值 |
等差数列{an}的公差d < 0,且a2a4 = 12,a2 + a4 = 8,则数列{an}的通项公式是( )
| A.an = 2n-2 (n∈N*) | B.an =" 2n" + 4 (n∈N*) |
| C.an =-2n + 12 (n∈N*) | D.an =-2n + 10 (n∈N*) |
在等差数列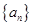 中,
中,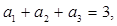
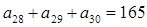 ,则此数列前30项和等于( )
,则此数列前30项和等于( )
| A.810 | B.840 | C.870 | D.900 |
若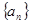 为等差数列,
为等差数列,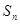 是其前
是其前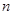 项和,且
项和,且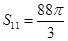 ,则
,则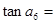 ( )
( )
A.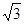 | B.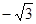 | C. | D.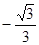 |
已知数列 满足:
满足: ,
, ,
, ,那么使
,那么使 成立的
成立的 的最大值为( )
的最大值为( )
| A.4 | B.5 | C.24 | D.25 |
首项为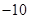 的等差数列,从第
的等差数列,从第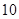 项起开始为正数,则公差
项起开始为正数,则公差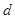 的取值范围是( ).
的取值范围是( ).
A. | B.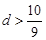 | C.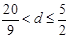 | D.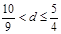 |
数列{an}是公差不为0的等差数列,a1=1且a1、a3、a6成等比数列,则{an}的前n项和Sn等于( )
A.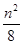 + + | B.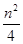 + +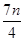 |
C.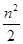 + +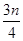 | D.n2+n |
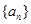 的前
的前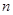 项和
项和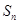 ,若
,若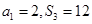 ,则
,则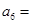 ( )
( )