题目内容
若数列{an}是等比数列,且an>0,则数列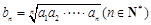 也是等比数列. 若数列
也是等比数列. 若数列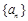 是等差数列,可类比得到关于等差数列的一个性质为( ).
是等差数列,可类比得到关于等差数列的一个性质为( ).
A.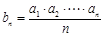 是等差数列 是等差数列 |
B.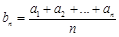 是等差数列 是等差数列 |
C.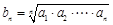 是等差数列 是等差数列 |
D.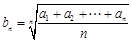 是等差数列 是等差数列 |
B
解析试题分析:本题是由等比数列与等差数列的相似性质,推出有关结论:由“等比”类比到“等差”,由“几何平均数”类比到“算数平均数”;所以,所得结论为 是等差数列.
是等差数列.
考点:类比推理.

练习册系列答案
 导学与测试系列答案
导学与测试系列答案 新非凡教辅冲刺100分系列答案
新非凡教辅冲刺100分系列答案
相关题目
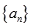 为等差数列,
为等差数列,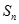 为前
为前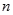 项和,
项和,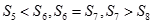 ,则下列错误的是( ).
,则下列错误的是( ).
A. | B. |
C. | D. 和 和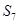 均为 均为 的最大值 的最大值 |
已知等差数列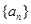 的前
的前 项和为
项和为 ,若
,若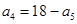 ,则
,则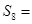 ( )
( )
A.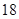 | B. | C. | D.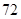 |
已知等差数列 的公差
的公差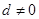 ,且
,且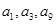 成等比数列,则
成等比数列,则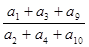 的值是( )
的值是( )
A.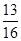 | B.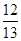 | C.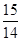 | D.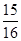 |
等差数列 的第15项为( )
的第15项为( )
| A.53 | B.40 | C.63 | D.76 |
等差数列{an}的公差d < 0,且a2a4 = 12,a2 + a4 = 8,则数列{an}的通项公式是( )
| A.an = 2n-2 (n∈N*) | B.an =" 2n" + 4 (n∈N*) |
| C.an =-2n + 12 (n∈N*) | D.an =-2n + 10 (n∈N*) |
在等差数列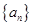 中,
中,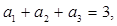
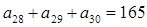 ,则此数列前30项和等于( )
,则此数列前30项和等于( )
| A.810 | B.840 | C.870 | D.900 |
已知数列 满足:
满足: ,
, ,
, ,那么使
,那么使 成立的
成立的 的最大值为( )
的最大值为( )
| A.4 | B.5 | C.24 | D.25 |
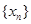 ,从中选取若干项,不改变它们在原来数列中的先后次序,得到的数列称为是原来数列的一个子数列. 某同学在学习了这一个概念之后,打算研究首项为
,从中选取若干项,不改变它们在原来数列中的先后次序,得到的数列称为是原来数列的一个子数列. 某同学在学习了这一个概念之后,打算研究首项为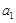 ,公差为
,公差为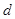 的无穷等差数列
的无穷等差数列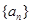 的子数列问题,为此,他取了其中第一项
的子数列问题,为此,他取了其中第一项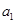 ,第三项
,第三项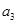 和第五项
和第五项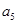 .
. 成等比数列,求
成等比数列,求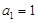 ,
, 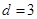 的无穷等差数列
的无穷等差数列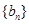 ,使得数列
,使得数列 ,公比为正整数
,公比为正整数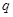 (
(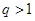 )的无穷等比数 列
)的无穷等比数 列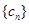 ,总可以找到一个子数列
,总可以找到一个子数列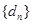 ,使得
,使得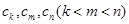 ,由
,由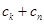 与
与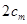 的大小关系去判断该命题是否正确. 他将得到什么结论?
的大小关系去判断该命题是否正确. 他将得到什么结论?