题目内容
【题目】已知数列![]() 和
和![]() 满足:
满足:![]() ,
,![]() ,
,![]() 且对一切
且对一切![]() ,均有
,均有![]() .
.
(1)求证:数列![]() 为等差数列,并求数列
为等差数列,并求数列![]() 的通项公式;
的通项公式;
(2)求数列![]() 的前
的前![]() 项和
项和![]() ;
;
(3)设![]() ,记数列
,记数列![]() 的前
的前![]() 项和为
项和为![]() ,求正整数
,求正整数![]() ,使得对任意
,使得对任意![]() ,均有
,均有![]() .
.
【答案】(1)证明见解析;(2)![]() ;(3)
;(3)![]() .
.
【解析】
(1)在等式![]() 两边同时除以
两边同时除以![]() ,可得出
,可得出![]() ,利用等差数列的定义可证明出数列
,利用等差数列的定义可证明出数列![]() 为等差数列,求出数列
为等差数列,求出数列![]() 的通项公式,可得出数列
的通项公式,可得出数列![]() 的通项公式;
的通项公式;
(2)先求出![]() 的值,由
的值,由![]() 时,由
时,由![]() ,可得出
,可得出![]() ,两式相除可得出
,两式相除可得出![]() 的表达式,再对
的表达式,再对![]() 是否满足
是否满足![]() 在
在![]() 的表达式,即可得出数列
的表达式,即可得出数列![]() 的通项公式,再利用等比数列的求和公式求出
的通项公式,再利用等比数列的求和公式求出![]() ;
;
(3)令![]() ,利用数列的单调性求出满足
,利用数列的单调性求出满足![]() 的最大整数
的最大整数![]() 的值为
的值为![]() ,即可得出结论.
,即可得出结论.
(1)由![]() ,
,![]() ,
,
两边除以![]() ,得
,得![]() ,即
,即![]() ,所以,数列
,所以,数列![]() 为等差数列.
为等差数列.
![]() ,所以,
,所以,![]() ;
;
(2)当![]() 时,
时,![]() .
.
对任意的![]() ,
,![]() ,则
,则![]() ;
;
当![]() 时,由
时,由![]() 可得
可得![]() ,
,
两式相除得![]() ,
,
![]() 满足
满足![]() ,所以,对任意的
,所以,对任意的![]() ,
,![]() ,
,![]() ,
,
即数列![]() 是公比为
是公比为![]() 的等比数列,且首项为
的等比数列,且首项为![]() ,因此,
,因此,![]() ;
;
(3)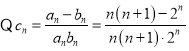 ,令
,令![]() ,即
,即![]() ,即
,即![]() ,
,
构造数列![]() ,则
,则![]() ,
,
当![]() 时,则有
时,则有![]() ,即
,即![]() ;
;
当![]() 时,
时,![]() ;
;
当![]() 时,
时,![]() ,即
,即![]() ,可得
,可得![]() .
.
所以,数列![]() 最大项的值为
最大项的值为![]() ,又
,又![]() ,
,![]() ,
,![]()
当![]() 时,
时,![]() .
.
所以,当![]() 时,
时,![]() ,此时
,此时![]() ;当
;当![]() 时,
时,![]() ,此时
,此时![]() .
.
综上所述,数列![]() 中,
中,![]() 最大,因此,
最大,因此,![]() .
.

练习册系列答案
 智趣寒假作业云南科技出版社系列答案
智趣寒假作业云南科技出版社系列答案
相关题目